Circles

9 Components
Initial Task
Square Peg
Big Ideas
Big Idea 1 Big Idea 2 Big Idea 3
Formative Assessment Lesson
Inscribing and Circumscribing Right Triangles
Re-engagement
Re-engagement for Unit 7
End of Unit Assessments
End of Unit Assessment for Unit 7 End of Unit Assessment Teacher Resources for GEO Unit 7 Find aligned Regents questions with Quiz Banker
Geo U6: Circles
Browse Components
Initial Task
Square Peg
Big Ideas
Big Idea 1 Big Idea 2 Big Idea 3
Formative Assessment Lesson
Inscribing and Circumscribing Right Triangles
Re-engagement
Re-engagement for Unit 7
End of Unit Assessments
End of Unit Assessment for Unit 7 End of Unit Assessment Teacher Resources for GEO Unit 7 Find aligned Regents questions with Quiz Banker
Big Idea:

Big Idea 1

A circle is uniquely defined in the coordinate plane using its center and radius.

1 week
See Standards
Common Core: Major Standards:
G-GPE.B.4

Use coordinates to prove simple geometric theorems algebraically. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, 2).

G-SRT.B.5

Prove theorems involving similarity. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. Clarification: ASA, SAS, SSS, AAS, and Hypotenuse-Leg theorem are valid criteria for triangle congruence. AA, SAS, and SSS are valid criteria for triangle similarity.

Common Core: Supporting Standards:
G-CO.D.12

Make geometric constructions. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. Clarification: Constructions include but are not limited to the listed constructions. Example: constructing the median of a triangle or constructing an isosceles triangle with given lengths.

Common Core: Additional Standards:
G-GPE.A.1

Translate between the geometric description and the equation for a conic section. Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation.

G-C.A.1

Understand and apply theorems about circles. Prove that all circles are similar.

Evidence of Understanding

  • describe the characteristics of any circle
    • construct a circle using a compass and justify that all radii are equidistant and congruent
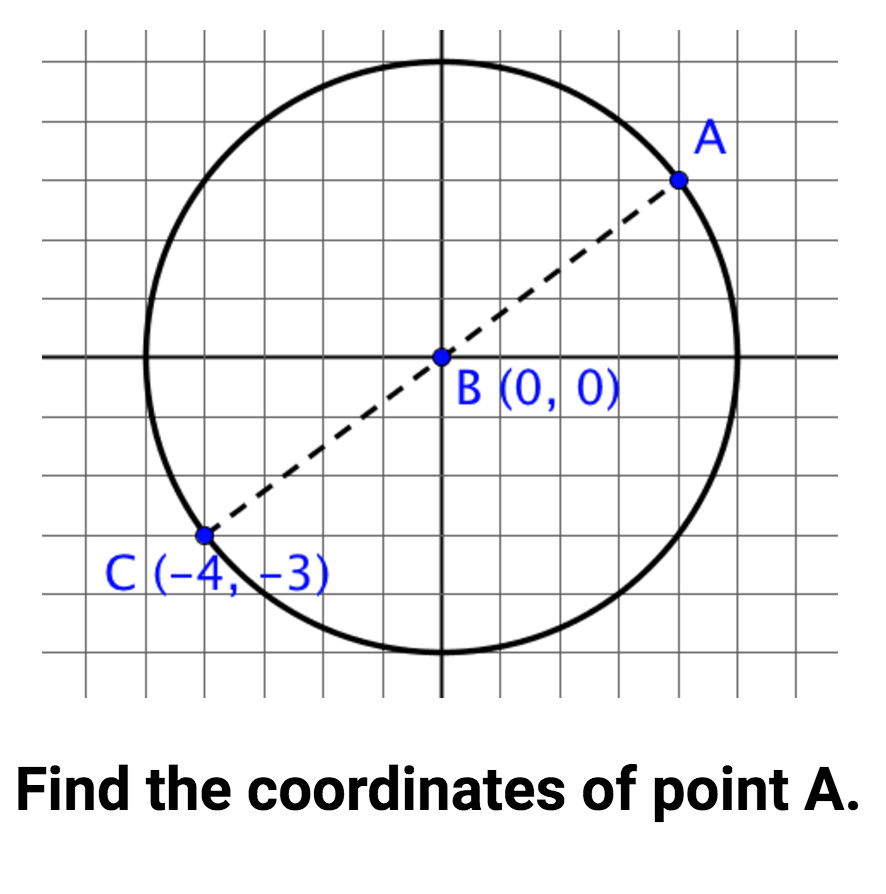
    • explain that all points on the circle are equidistant from the center of the circle
    • define radius as a relationship between a circle’s center and points on the circle
      • justify circles are similar using scale factor
      • reason proportionally and connect the measurements of a circle with similarity
    • analyze examples and non-examples to distinguish radii, chords, tangents, and secants
    • use constructions to explain the relationship between the radius and a tangent line
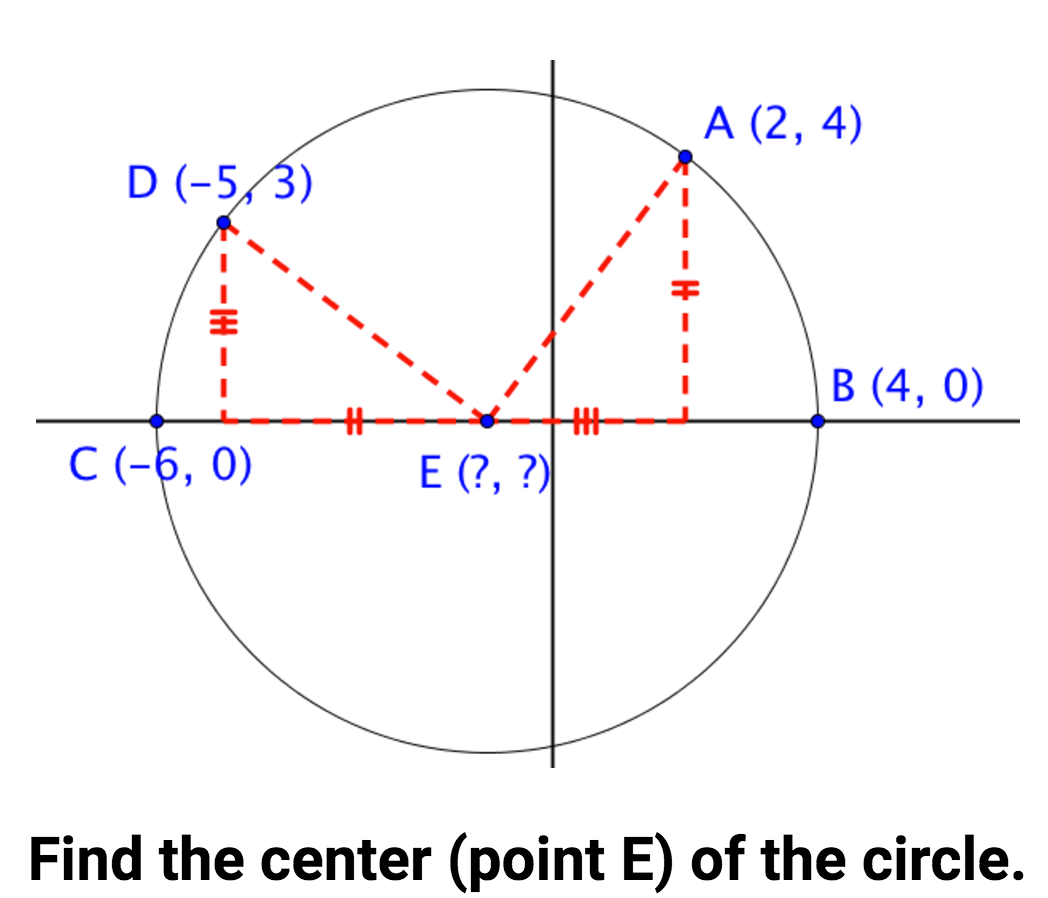
    • construct perpendicular bisectors of chords to show they always pass through the circle’s center
  • analyze characteristics of a circle in the coordinate plane
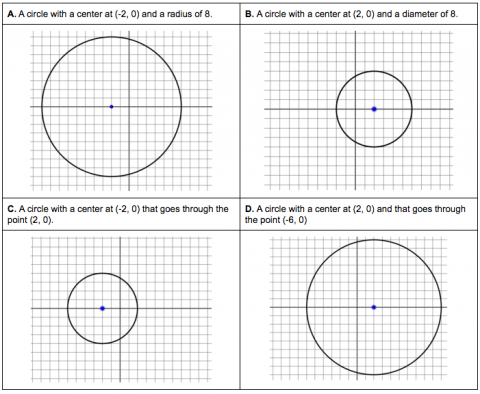
    • graph a circle in the coordinate plane given its center and radius
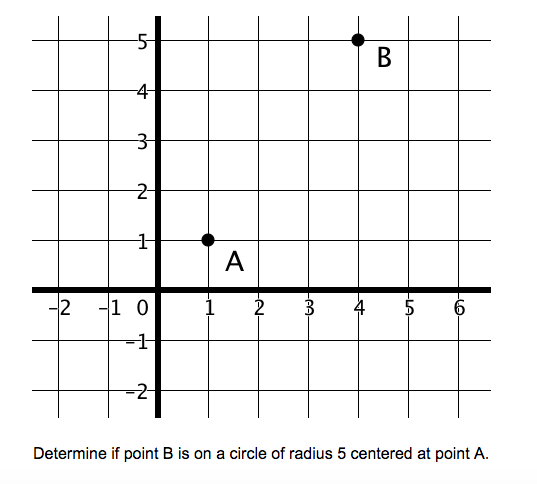
    • explore whether a point lies on a circle whose radius and center point are known
      • identify and justify possible methods including the use of a compass, straightedge, the Pythagorean Theorem, the distance formula, etc.
    • prove whether a point lies on a circle given the circle’s center and another point on the circle
    • describe characteristics about a circle given its center, radius, points on the circle, etc.
      • Example: find the area of a circle whose endpoints of its diameter lie at (2, 3) and (10, -3), or determine the diameter of a circle centered at the origin and passing through (-5, 10)
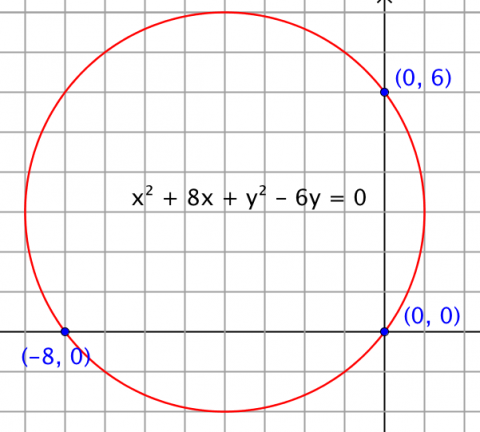
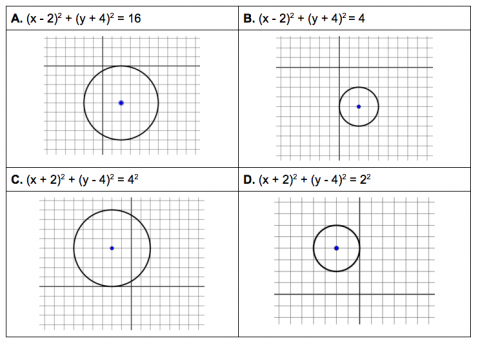
  • determine the standard equation of a circle in the coordinate plane
    • describe connections between a circle’s equation and and its graph in the coordinate plane
    • generate the equation of a circle from its graph
    • derive the equation of a circle from the Pythagorean Theorem
      • describe the relationship between x, h, y, k,r and the Pythagorean Theorem
    • generate a circle’s equation given information about its center, radius, or points on the circle
    • apply completing the square to write the equation of a circle in standard form

Develop conceptual understanding:

circle, radius/radii, equidistant, center of the circle, points on the circle, equation of a circle

Supporting terms to communicate:

similar, scale factor, coordinates, Pythagorean Theorem, completing the square

Core Resource

A core resource supports multiple days of instruction.

  • Defining Circles
    This incomplete Core Resource supports students in making connections between the Pythagorean theorem and the equation of circles.
    Resource:
    Defining Circles

    Geometry & Algebra II Archive

    Geo U6: Circles

    Big Idea: Big Idea 1

    This incomplete Core Resource supports students in making connections between the Pythagorean theorem and the equation of circles.

    Preview ResourceAdd a Copy of Resource to my Google Drive
    Type
    Geometry: Circles
    File
    Google Doc
    Tags
    circle, equation
    Standards
    Common Core: Major Standards ( G-SRT.B.5, G-GPE.B.4 ) Common Core: Supporting S…
    +— Details
    Common Core: Major Standards:
    G-SRT.B.5

    Prove theorems involving similarity. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. Clarification: ASA, SAS, SSS, AAS, and Hypotenuse-Leg theorem are valid criteria for triangle congruence. AA, SAS, and SSS are valid criteria for triangle similarity.

    G-GPE.B.4

    Use coordinates to prove simple geometric theorems algebraically. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, 2).

    Common Core: Supporting Standards:
    G-CO.D.12

    Make geometric constructions. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. Clarification: Constructions include but are not limited to the listed constructions. Example: constructing the median of a triangle or constructing an isosceles triangle with given lengths.

    Common Core: Additional Standards:
    G-C.A.1

    Understand and apply theorems about circles. Prove that all circles are similar.

    G-GPE.A.1

    Translate between the geometric description and the equation for a conic section. Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation.

    All Resources From:
Instructional Routine: Sharing Skepticism

The primary goal of this instructional routine is to support students in constructing and critiquing mathematical arguments.