Evidence of Understanding
- analyze distance in the coordinate plane and use distance to relate points and lines
- calculate the distance between two points using the Pythagorean Theorem
- generalize methods for determining the distance between two coordinate points
- derive the distance formula using a right triangle and the Pythagorean Theorem
- explain how the distance formula and Pythagorean Theorem can both be used to find length measurements of segments (or sides of a geometric figure)
- partition a segment using any point on the segment and find the ratio of its parts
- describe connections between the partition ratio, dilation, and scale factor
- given a specified ratio, find the coordinates of a point that partitions a line segment
- find the coordinates of a segment’s midpoint
- prove the midpoint of a segment creates two congruent lengths
- recognize that partitioning a segment with its midpoint bisects the segment in a 1:1 ratio
- describe direction in the coordinate plane and use direction to relate points and lines
- given two points, determine the direction of the line containing the two points
- generalize methods for determining the direction between two coordinate points
- generate and describe the slope formula using a right triangle
- dilate a line segment or line and analyze connections between the pre-image and its image
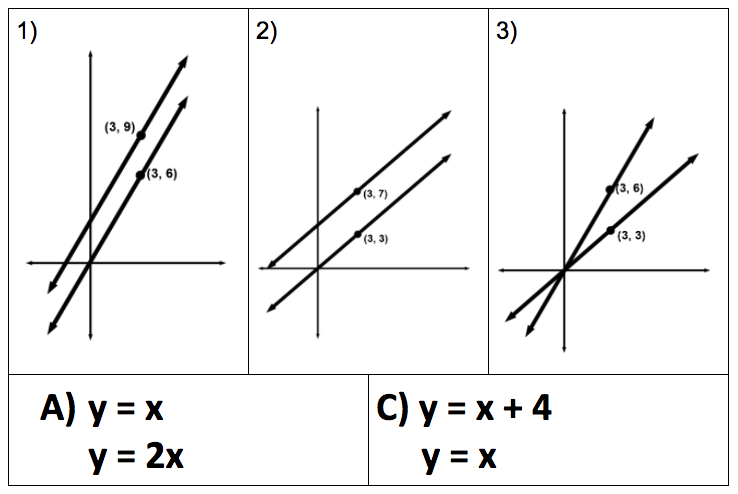
- make conjectures and use tools to prove parallel lines have the same slope
- describe connections between parallel lines, dilation, and scale factor
- rotate a line and analyze the relationship between the slope of the original line and its image
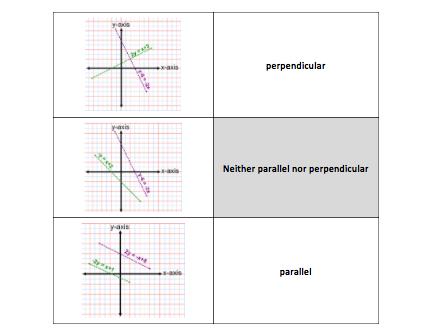
- show if slopes of two lines have a product of negative one, then they are perpendicular
- identify and justify if two lines are parallel or perpendicular
- create equations that represent parallel lines or perpendicular lines
- given the equation of a line and a specified transformation, determine the equation of its image or pre-image on the coordinate plane
Develop conceptual understanding:
distance formula, partition, midpoint, direction, slope formula, parallel, perpendicular
Supporting terms to communicate:
Pythagorean Theorem, ratio, bisect, dilation, scale factor, similarity, proportion, reciprocal, congruent, rotation