Evidence of Understanding
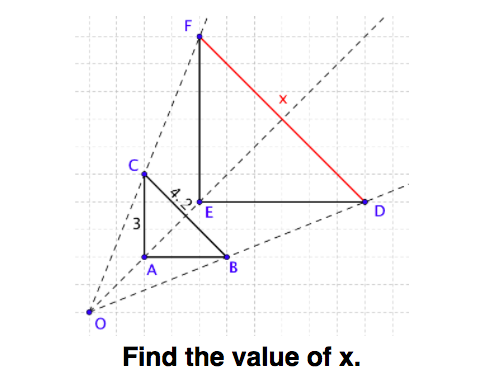
- describe the center of dilation as the vertex of an angle
- experiment and describe relationships involving the center of dilation by constructing line segments or figures along the two rays
- explain why dilated lines not passing through the center of dilation are parallel and dilated lines passing through the center of dilation are superimposed
- identify and justify the center of dilation between dilated figures
- describe angle relationships using properties of parallel lines cut by a transversal
- describe angle relationships using properties of parallel lines cut by a transversal
- analyze relationships between corresponding sides and corresponding angles of dilated figures
- use tools to create and describe features of figures that are enlarged or reduced
- identify, using markings, corresponding angles that are congruent (ratio is always 1:1)
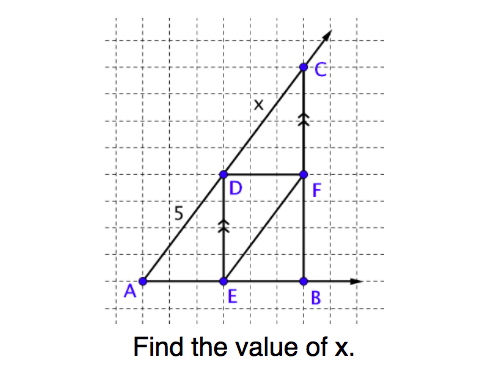
- explain the proportional relationship between corresponding sides of a pre-image and its image
- analyze the impacts of a dilation between dilated figures
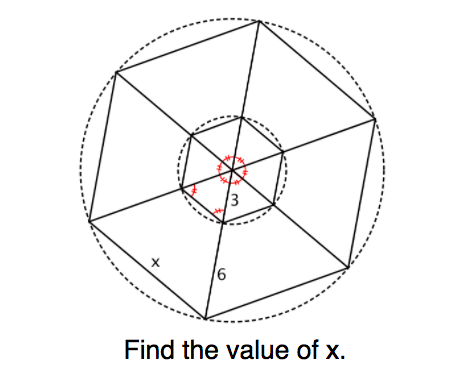
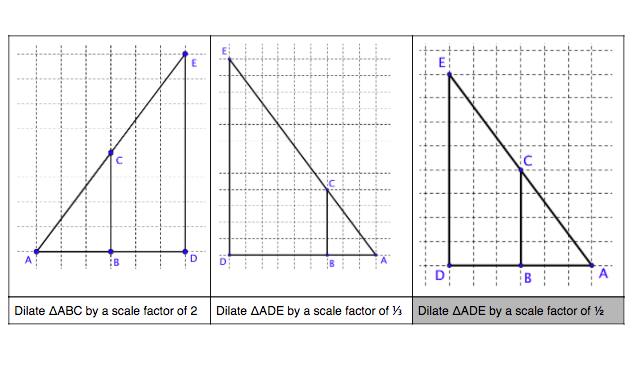
- determine the scale factor between a given preimage and image
- apply the scale factor to determine measurements of a pre-image or its image
- explain why perimeter maintains the scale factor and area squares the scale factor
- determine the minimum criteria that proves polygons are similar (focusing on triangles)
- transform figures to distinguish and define congruence and similarity
- use the equality of all corresponding pairs of angles (same shape) and the proportionality of all corresponding pairs of sides (scale factor) to define similarity
- use coordinate notation with the plane to describe transformations
- identify the triangles, quadrilaterals, and other polygons that are always similar, sometimes similar or never similar and explain reasoning
- use tools and counterexamples to justify Angle-Angle (AA) is valid criteria for triangle similarity
- use the triangle angle sum theorem to describe why AA is sufficient minimum criteria
- compare the Side-Angle-Side (SAS) and Side-Side-Side (SSS) criteria for congruence proofs versus similarity proofs
- use tools and counterexamples to justify that two proportional sides and the congruent included angle is sufficient criteria for proving two triangles are similar
- justify why criteria for triangle congruence are also sufficient for proving triangle similarity
- explain congruence as a special case of similarity where the scale factor is 1
- transform figures to distinguish and define congruence and similarity
Develop conceptual understanding:
dilation, center of dilation, ratio, proportional, scale factor, perimeter, area, similarity, AA, SAS, SSS, congruenceSupporting terms to communicate:
vertex, angle, segment, ray, corresponding, enlarge, reduce, parallel, transversal, preimage, image, transformation, rotation, reflection, translation