Similarity and Proof

9 Components
Initial Task
Triangles
Big Ideas
Big Idea 1 Big Idea 2 Big Idea 3
Formative Assessment Lesson
Identifying Similar Triangles
Re-engagement
Re-engagement for Unit 3
End of Unit Assessments
End of Unit Assessment for Unit 3 End of Unit Assessment Teacher Resources for GEO Unit 3 Find aligned Regents questions with Quiz Banker
Geo U3: Similarity and Proof
Browse Components
Initial Task
Triangles
Big Ideas
Big Idea 1 Big Idea 2 Big Idea 3
Formative Assessment Lesson
Identifying Similar Triangles
Re-engagement
Re-engagement for Unit 3
End of Unit Assessments
End of Unit Assessment for Unit 3 End of Unit Assessment Teacher Resources for GEO Unit 3 Find aligned Regents questions with Quiz Banker
Big Idea:

Big Idea 2

Congruent corresponding angles and proportional corresponding sides are used to prove triangles are similar.

1 week
See Standards
Common Core: Major Standards:
G-CO.C.10

Prove geometric theorems. Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. Clarification: Theorems include but are not limited to the listed theorems. Example: an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles of the triangle

G-SRT.B.5

Prove theorems involving similarity. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. Clarification: ASA, SAS, SSS, AAS, and Hypotenuse-Leg theorem are valid criteria for triangle congruence. AA, SAS, and SSS are valid criteria for triangle similarity.

G-SRT.B.4

Prove theorems involving similarity. Prove theorems about triangles. Theorems include: a line parallel to one side of a triangle divides the other two proportionally, and conversely; the Pythagorean Theorem proved using triangle similarity. Clarification: Theorems include but are not limited to the listed theorems. Example: the length of the altitude drawn from the vertex of the right angle of a right triangle to its hypotenuse is the geometric mean between the lengths of the two segments of the hypotenuse.

G-SRT.A.2

Understand similarity in terms of similarity transformations. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.

Common Core: Supporting Standards:
G-CO.A.5

Experiment with transformations in the plane. Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.

G-CO.D.12

Make geometric constructions. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. Clarification: Constructions include but are not limited to the listed constructions. Example: constructing the median of a triangle or constructing an isosceles triangle with given lengths.

Evidence of Understanding

  • prove triangles are similar and solve problems in geometric figures using congruence and similarity criteria for triangles
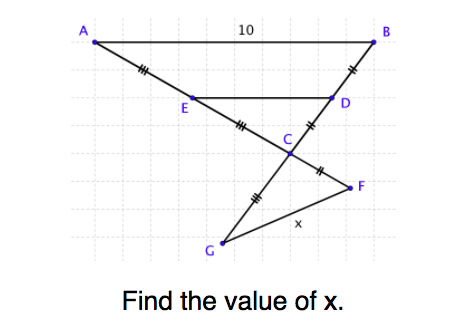
    • use markings and notations to identify congruent corresponding angles and proportional corresponding sides of triangles
      • map figures onto one another in the plane and identify corresponding angles and sides
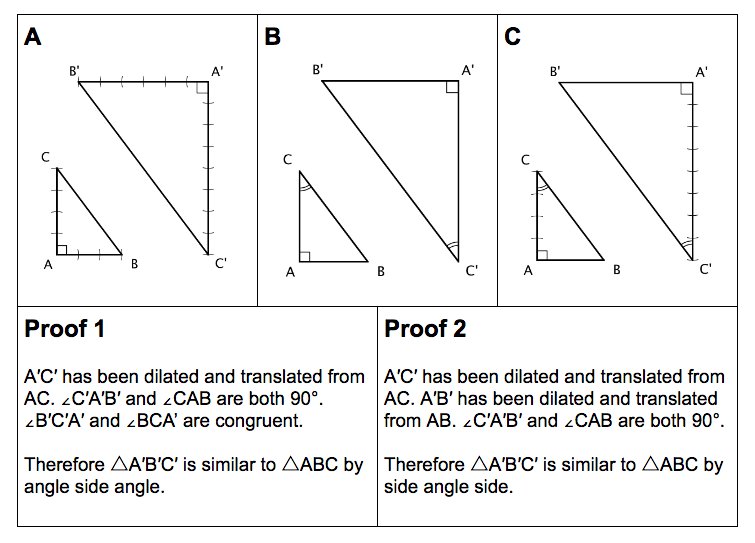
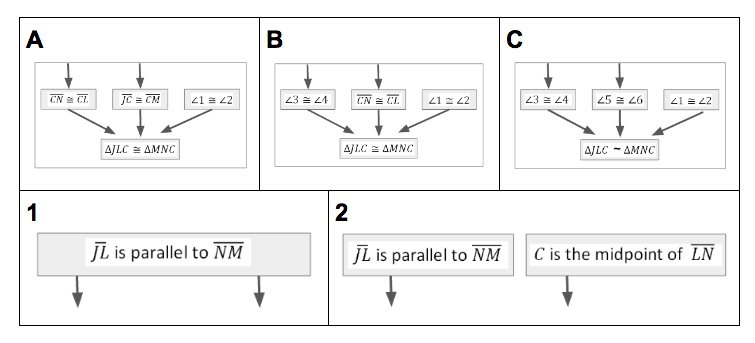
    • use information about triangle similarity and congruence to determine which information is required to prove figures are similar
      • apply transformations to re-draw figures and explain the corresponding relationships between the two diagrams drawn
      • explain the angle where the center of dilation is the vertex using reflexive property
      • apply properties of parallel lines to prove figures are similar
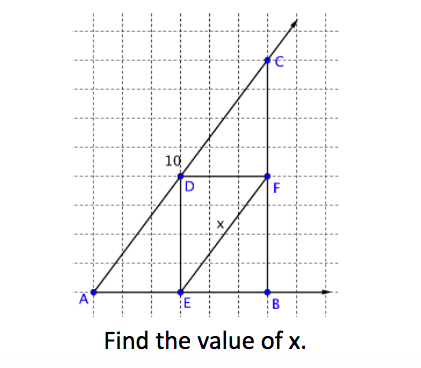
    • find missing values by applying the relationships of sides (scale factor) and angles
  • prove characteristics about the midsegment of a triangle
    • construct and make conjectures about the relationship that forms by creating the midsegment
    • prove that the midsegment is parallel to one side of a triangle and divides the other two proportionally
      • prove that midsegments have the same relationship in quadrilaterals
    • use midsegments to prove relationships between figures and find missing measurements
  • prove characteristics about the medial triangle (also called the midpoint triangle)
    • construct a medial triangle and make conjectures about the relationships of triangles formed
    • apply properties of parallel lines to prove similarity and congruence relationships between the larger triangle and the other triangles created within it
      • prove the medial triangle (or one of the other three) is similar to the larger triangle
      • prove the medial triangle is congruent to the other 3 triangles created within the larger triangle

Develop conceptual understanding:

scale factor, midsegment, medial or midpoint triangle

Supporting terms to communicate:

proportional, ratio, corresponding, dilation, center of dilation, rotation, reflection, translation, vertex, similarity, congruence, AA, SAS, ASA, AAS, SSS, midpoint, bisect, parallel, partition
Core Resource

No Core Resource for this Big Idea.

Consider using the Instructional Routines linked below for teaching towards this Big Idea.