Evidence of Understanding
- explore and prove qualities about the interior and exterior angles of any triangle
- use examples and nonexamples to determine when an angle within a triangle can be classified as interior or exterior
- analyze examples to justify that interior angles always add up to 180° and the exterior angles add up to 360° and attempt to create counterexamples
- use tools to draw triangles and measure angles, and explain the impact of human error in this process
- describe and classify triangles based on their angle measures (right, acute, obtuse)
- describe how the relationships between interior angles of a triangle impact its corresponding side lengths and classification (equilateral, isosceles, scalene)
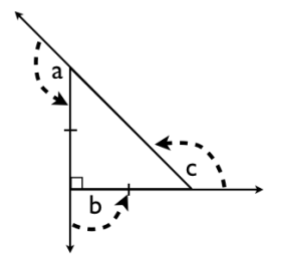
- use deductive reasoning to prove that, for any triangle, the three interior angles add up to 180° and the three exterior angles add up to 360°
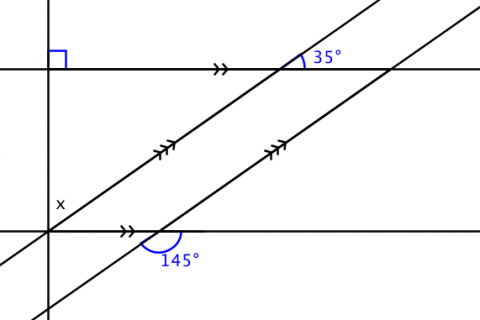
- draw or construct auxiliary lines and apply the properties of parallel lines
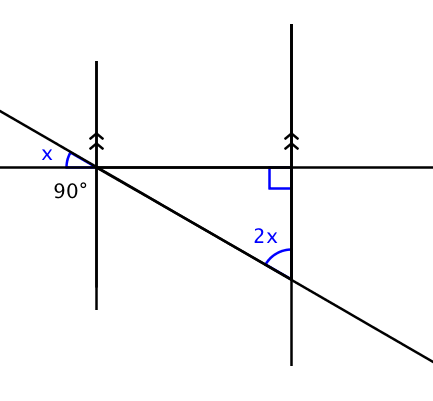
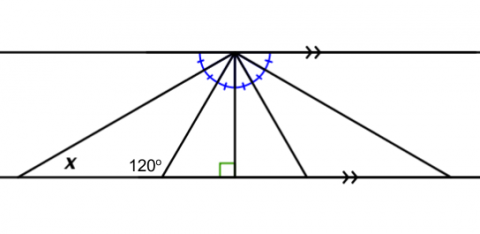
- find the values of missing interior angles of a triangle
- identify and describe relationships between the interior and exterior angles of a triangle
- analyze examples to justify thatthe exterior angle is always equal to the sum of the two remote angles and attempt to create counterexamples
- use deductive reasoning to prove that the exterior angle is always equal to the sum of the two remote angles
- describe the reflexive and transitive properties when using triangle sum and linear pair in the proof
- find the measure of missing interior or exterior angles
Develop conceptual understanding:
Interior, exterior, triangle, isosceles, equilateral, scalene, right, acute, obtuse, example, nonexample, interior angles of a triangle, exterior angles of a triangle, remote interior angles (non-adjacent interior angles), auxiliary line, counterexampleSupporting terms to communicate:
side lengths, angle measure, congruent, construct, supplementary, complementary, congruent, straight angles, reflexive property, transitive property, substitute, adjacent