Evidence of Understanding
- describe the criteria for congruence and justify why corresponding parts of congruent triangles must be congruent (CPCTC)
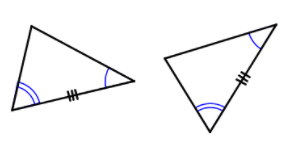
- identify corresponding parts of congruent triangles
- write congruence statements based on notations in a diagram
- re-draw and re-orient diagrams to highlight corresponding parts of congruent triangles
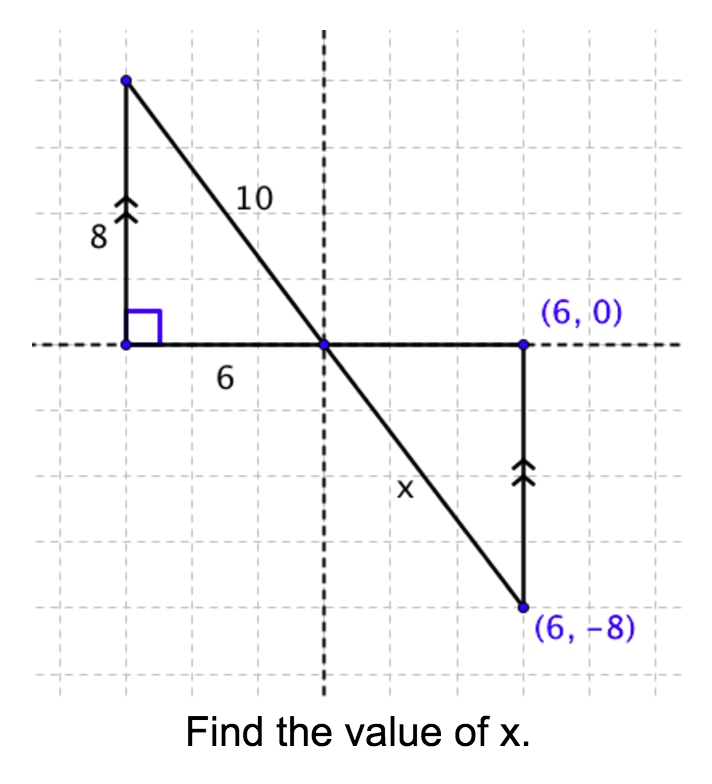
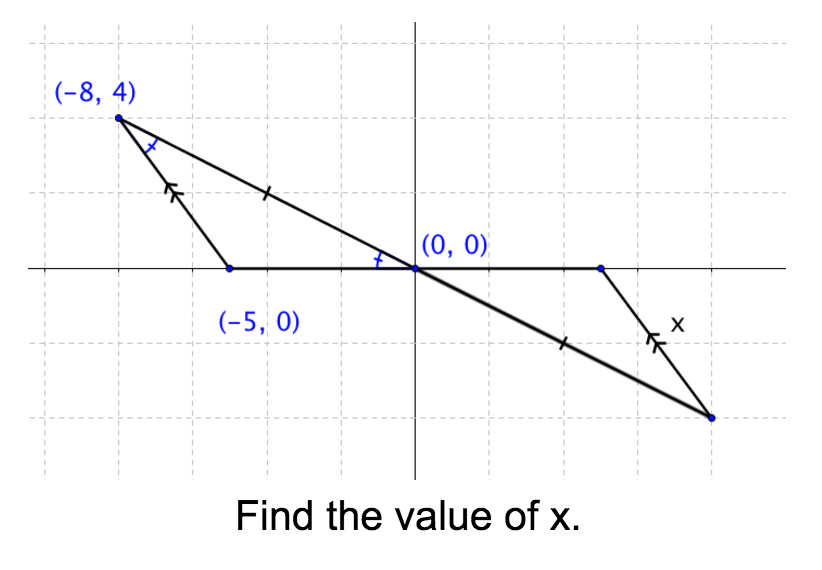
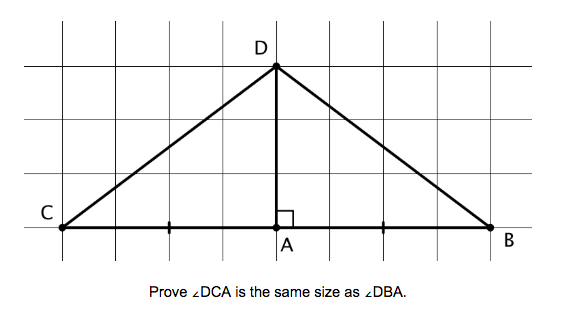
- prove two triangles are congruent
- explain the congruence between two triangles using rigid motion transformations or constructions
- identify corresponding congruent parts and apply the criteria of SSS, SAS, ASA, or AAS
- prove two right triangles are congruent when corresponding Hypotenuse-Leg (HL) are congruent
- discern when and how to use definitions and the transitive and reflexive properties to establish necessary criteria to prove two triangles are congruent
- decompose polygons, parallelograms, and triangles to prove congruence
- prove that the base angles of an isosceles triangle are congruent
- apply CPCTC to prove that the opposite angles (base angles) of the given sides are congruent
- prove a parallelogram is composed of two congruent triangles
- explore and describe when a parallelogram is composed of four congruent triangles
- prove that a regular hexagon is composed of 6 congruent, equilateral triangles
- prove that the base angles of an isosceles triangle are congruent
Develop conceptual understanding:
corresponding parts of congruent triangles are congruent (CPCTC), SSS, ASA, AAS, SAS, Hypotenuse-Leg, base angles, perpendicular bisector, opposite angle/side, parallelogram
Supporting terms to communicate:
corresponding, construct, rotate, reflect, translate, triangle, isosceles, equilateral, scalene, right, acute, obtuse, congruence, equidistant, reflexive property, transitive property, parallel