Evidence of Understanding
- investigate the relationship between the diagonals of a quadrilateral and its other characteristics
-
analyze examples and nonexamples to make conjectures about diagonals belonging to parallelograms, rectangles, squares, trapezoids, kites, and rhombuses
- use constructions, paper folding, and other tools to justify diagonals: of a parallelogram bisect each other, of a rectangle are congruent, and kites are perpendicular
- construct a square inscribed in a circle using perpendicular bisectors
-
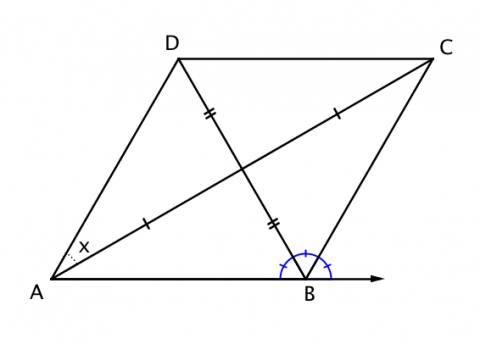
prove diagonals of parallelograms bisect each other
- prove the converse statement (if diagonals bisect each other then it is a parallelogram)
- use CPCTC to deductively prove the diagonals intersect at their midpoint
-
prove diagonals of rectangles are congruent
- investigate diagonals of an isosceles trapezoid and use them show the converse statement is false
-
prove diagonals of a rhombus perpendicularly bisect one another
- demonstrate perpendicular diagonals do not necessarily bisect one another (ex: kites)
- find the measure of the missing length of a diagonal
-
analyze examples and nonexamples to make conjectures about diagonals belonging to parallelograms, rectangles, squares, trapezoids, kites, and rhombuses
Develop conceptual understanding:
parallelogram, rectangle, square, trapezoid, kite, rhombus, inscribedSupporting terms to communicate:
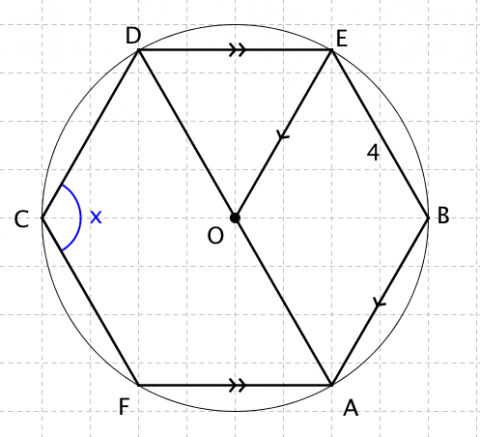
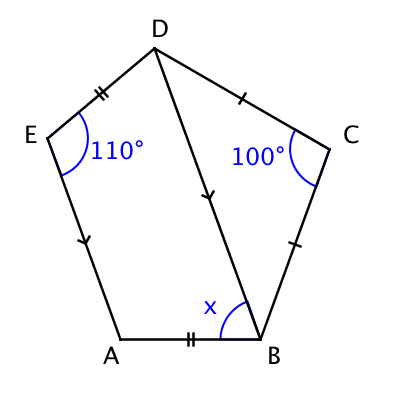
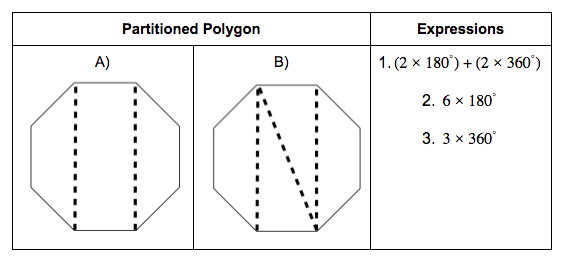
trapezoid, diagonal, congruent, bisect, perpendicular, midpoint, segment, sides, lengths, measure, CPCTC, converse, polygon, pentagon, hexagon, octagon, interior angle, exterior angle