Right Triangle Trigonometry

8 Components
Initial Task
Hopewell Geometry
Big Ideas
Big Idea 1 Big Idea 2
Formative Assessment Lesson
Proofs of the Pythagorean Theorem
Re-engagement
Re-engagement for Unit 4
End of Unit Assessments
End of Unit Assessment for Unit 4 End of Unit Assessment Teacher Resources for GEO Unit 4 Find aligned Regents questions with Quiz Banker
Geo U4: Right Triangle Trigonometry
Browse Components
Initial Task
Hopewell Geometry
Big Ideas
Big Idea 1 Big Idea 2
Formative Assessment Lesson
Proofs of the Pythagorean Theorem
Re-engagement
Re-engagement for Unit 4
End of Unit Assessments
End of Unit Assessment for Unit 4 End of Unit Assessment Teacher Resources for GEO Unit 4 Find aligned Regents questions with Quiz Banker
Big Idea:

Big Idea 1

Corresponding sides of similar triangles prove the Pythagorean Theorem is true for all right triangles.

1 week
See Standards
Common Core: Major Standards:
G-SRT.B.5

Prove theorems involving similarity. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. Clarification: ASA, SAS, SSS, AAS, and Hypotenuse-Leg theorem are valid criteria for triangle congruence. AA, SAS, and SSS are valid criteria for triangle similarity.

G-SRT.B.4

Prove theorems involving similarity. Prove theorems about triangles. Theorems include: a line parallel to one side of a triangle divides the other two proportionally, and conversely; the Pythagorean Theorem proved using triangle similarity. Clarification: Theorems include but are not limited to the listed theorems. Example: the length of the altitude drawn from the vertex of the right angle of a right triangle to its hypotenuse is the geometric mean between the lengths of the two segments of the hypotenuse.

Common Core: Additional Standards:
G-GMD.A.1

Explain volume formulas and use them to solve problems. Give an informal argument for the formulas for the circumference of a circle, area of a circle, volume of a cylinder, pyramid, and cone. (e.g. Use dissection arguments, Cavalieri’s principle, and informal limit arguments.)

G-GMD.A.3

Explain volume formulas and use them to solve problems. Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.★

Evidence of Understanding

  • use triangle similarity and scale factor to prove relationships for right triangles
    • prove the Pythagorean Theorem (proof of the Pythagorean theorem using similarity)
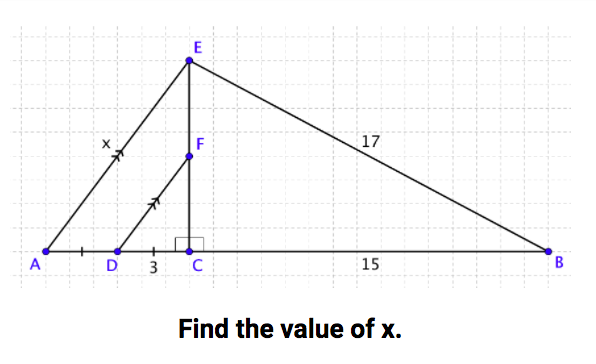
    • use similarity to analyze relationships between the altitude and the lengths of the two segments of the hypotenuse
      • prove the length of the altitude drawn from the vertex of the right angle is the geometric mean between the lengths of the two segments of the hypotenuse (video)
      • calculate the length of an altitude or one of the two segments of the hypotenuse
  • analyze characteristics of triangles using the Pythagorean Theorem
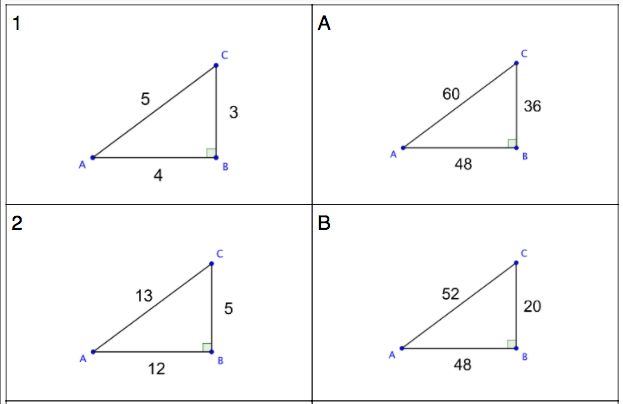
    • classify a triangle as acute, right, or obtuse using the Pythagorean theorem
      • use an area model to explain that when a2 + b2 > c2, the triangle is acute; that when a2 + b2  = c2, the triangle is right; and that when a2 + b2 < c2, the triangle is obtuse
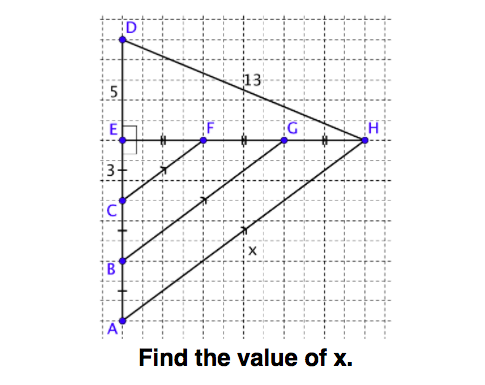
    • analyze and describe special Pythagorean triples using similarity and scale factor
      • explain that special triples occur when a2 + b2 is a perfect square and use this to strategically name Pythagorean triples
      • use similarity to explain and name other triangles that are similar to the 3-4-5, 5-12-13, 8-15-17, or other Pythagorean triples
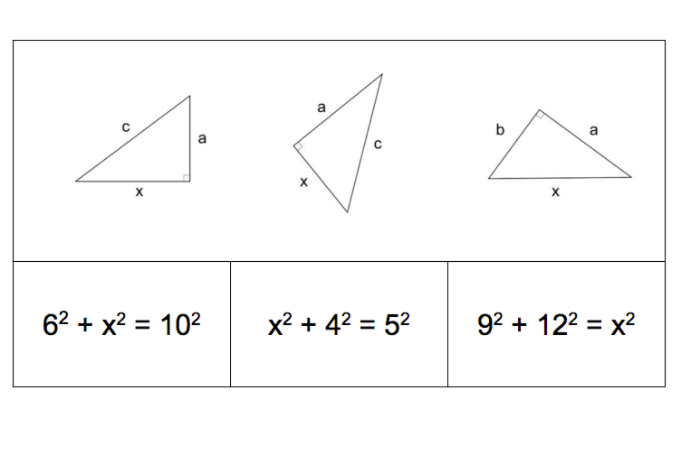
  • find the missing side length of a right triangle using Pythagorean Theorem
    • create diagrams to model situations and use Pythagorean Theorem to solve them
      • use right triangles and their properties to describe objects and/or situations
      • use properties of similar triangles and scale factor with the Pythagorean Theorem
    • use a Pythagorean triple, when applicable, to state missing side lengths

Develop conceptual understanding:

Pythagorean Theorem, geometric mean, acute triangle, obtuse triangle, right triangle, perfect square, Pythagorean triple

Supporting terms to communicate:

perpendicular, altitude, vertex, corresponding, leg, hypotenuse, right angle, acute angle, obtuse angle, similar, scale factor, proportional, ratio
Core Resource
A core resource supports multiple days of instruction.
  • Proving the Pythagorean Theorem
    Resource:
    Proving the Pythagorean Theorem

    Geometry & Algebra II Archive

    Geo U4: Right Triangle Trigonometry

    Big Idea: Big Idea 1

    <style type="text/css"><!--td {border: 1px solid #ccc;}br {mso-data-placement:same-cell;}--> </style> During this Core Resource, students explore the Pythagorean theorem and how similar triangles can be used in a variety of different ways to prove theorems about right triangles, including the Pythagorean theorem itself.

    Preview ResourceAdd a Copy of Resource to my Google Drive
    Type
    Geometry: Right Triangle Trigonometry
    File
    Google Doc
    Standards
    Common Core: Major Standards ( G-SRT.B.4, G-SRT.B.5 ) Common Core: Additional S…
    +— Details
    Common Core: Major Standards:
    G-SRT.B.4

    Prove theorems involving similarity. Prove theorems about triangles. Theorems include: a line parallel to one side of a triangle divides the other two proportionally, and conversely; the Pythagorean Theorem proved using triangle similarity. Clarification: Theorems include but are not limited to the listed theorems. Example: the length of the altitude drawn from the vertex of the right angle of a right triangle to its hypotenuse is the geometric mean between the lengths of the two segments of the hypotenuse.

    G-SRT.B.5

    Prove theorems involving similarity. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. Clarification: ASA, SAS, SSS, AAS, and Hypotenuse-Leg theorem are valid criteria for triangle congruence. AA, SAS, and SSS are valid criteria for triangle similarity.

    Common Core: Additional Standards:
    G-GMD.A.1

    Explain volume formulas and use them to solve problems. Give an informal argument for the formulas for the circumference of a circle, area of a circle, volume of a cylinder, pyramid, and cone. (e.g. Use dissection arguments, Cavalieri’s principle, and informal limit arguments.)

    G-GMD.A.3

    Explain volume formulas and use them to solve problems. Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.★

    All Resources From: