Evidence of Understanding
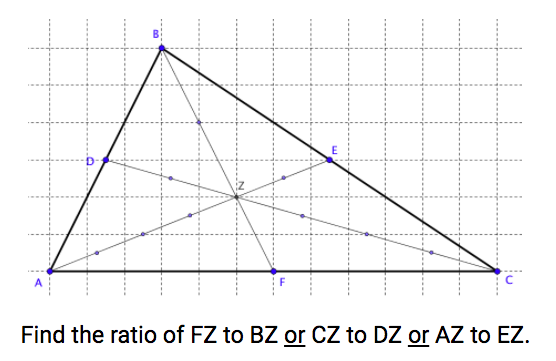
- construct medians and explain why they intersect at the centroid
- make conjectures about the relationship of the segment lengths that result from constructing 3 medians and prove that the segment lengths are in a ratio of 2:1
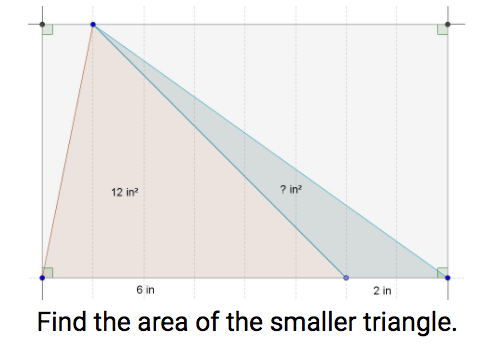
- make conjectures about the relationship of the areas of each triangle formed and prove they are the same (connection to center of mass)
- find missing values in a triangle that involve the median
- use tools and counterexamples to prove statements about triangles
- apply perpendicular bisectors to identify the circumcenter
- construct perpendicular bisectors and apply transformations to justify the location of the circumcenter
- make conjectures and justify why if two perpendicular bisectors intersect each other, then the third perpendicular bisector would intersect at the same point
- show the point of intersection is equidistant to the vertices of each side of the triangle it is perpendicularly bisecting
- show the point of intersection is equidistant to the vertices of each side of the triangle it is perpendicularly bisecting
- construct altitudes and use them to determine the orthocenter
- prove the triangles formed by constructing the altitude are similar
- analyze the relationship between the orthocenter of a medial triangle and the circumcenter of its larger triangle and prove why they are the same point
- explain how the perpendicular bisectors of the larger triangle are the same as the altitudes of the medial triangle
- make conjectures, using tools, about the location of the orthocenter in relationship to the triangle (right, acute, obtuse) and how the angle measures impact the location
- explain why the orthocenter of a right triangle always lies at the vertex of the triangle’s right angle
Develop conceptual understanding:
median, centroid, perpendicular bisectors, circumcenter, altitude, orthocenterSupporting terms to communicate:
vertex, midpoint, opposite side, proportional, ratio, scale factor, area, similar, equidistant, right, obtuse, acute, reflection, rotation, dilation, center of dilation, corresponding