Statistics (Inferences from Data)

8 Components
Initial Task
Animals
Big Ideas
Big Idea 1 Big Idea 2 Big idea 3
Formative Assessment Lesson
A Case of Muddying the Waters
Re-engagement
End of Unit Assessments
End of Unit Assessment for Unit 6 End of Unit Assessment Teacher Resources ALG II Unit 6 Find aligned Regents questions with Quiz Banker
A2 U6: Statistics (Inferences from Data)
Browse Components
Initial Task
Animals
Big Ideas
Big Idea 1 Big Idea 2 Big idea 3
Formative Assessment Lesson
A Case of Muddying the Waters
Re-engagement
End of Unit Assessments
End of Unit Assessment for Unit 6 End of Unit Assessment Teacher Resources ALG II Unit 6 Find aligned Regents questions with Quiz Banker
Big Idea:

Big Idea 1

Measures of center are used to interpret univariate data.

1 week
See Standards
Common Core: Supporting Standards:
S-ID.B.5

Summarize, represent, and interpret data on two categorical and quantitative variables.  Summarize categorical data for two categories in two‐way frequency tables. Interpret relative frequencies in the context of the data (including joint, marginal, and conditional relative frequencies). Recognize possible associations and trends in the data.

S-ID.B.6

Summarize, represent, and interpret data on two categorical and quantitative variables.  Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.

Common Core: Additional Standards:
S-ID.A.1

Summarize, represent, and interpret data on a single count or measurement variable. Represent data with plots on the real number line (dot plots, histograms, and box plots).

S-ID.A.2

Summarize, represent, and interpret data on a single count or measurement variable. Use statistics appropriate to the shape of the data distribution to compare center (median, mean) and spread (interquartile range, standard deviation) of two or more different data sets.

S-ID.A.3

Summarize, represent, and interpret data on a single count or measurement variable. Interpret differences in shape, center, and spread in the context of the data sets, accounting for possible effects of extreme data points (outliers).

S-ID.A.4

Summarize, represent, and interpret data on a single count or measurement variable. Use the mean and standard deviation of a data set to fit it to a normal distribution and to estimate population percentages. Recognize that there are data sets for which such a procedure is not appropriate. Use calculators, spreadsheets, and tables to estimate areas under the normal curve.

Evidence of Understanding

  • use mean, median, and mode to aggregate and interpret univariate data
    • describe what is gained and lost by interpreting a data set using the mean, median, or mode
    • describe how frequency and range impacts mean, median, and mode
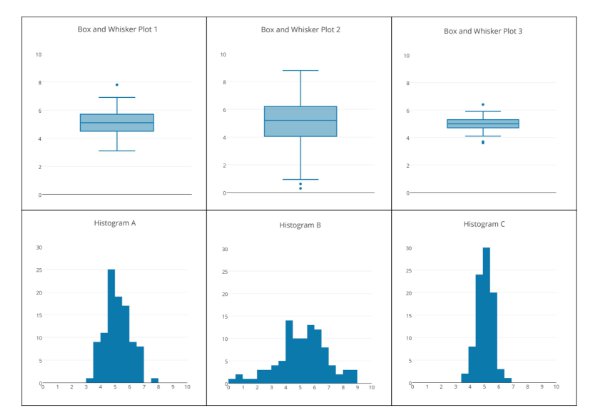
      • Interpret statistical representations such as box plots, dot pots, histograms, bar graphs, tables, etc. where some data points occur with a frequency > 1
    • describe how removing or adding a value to a data set impacts the mean and median
      • explain the effect of an extreme outlier on the mean compared to its effect on the median
    • identify which value(s) can be added to the data set that do not alter the median, mean, or mode and justify why
  • use range and density to describe how individual data points relate to the mean
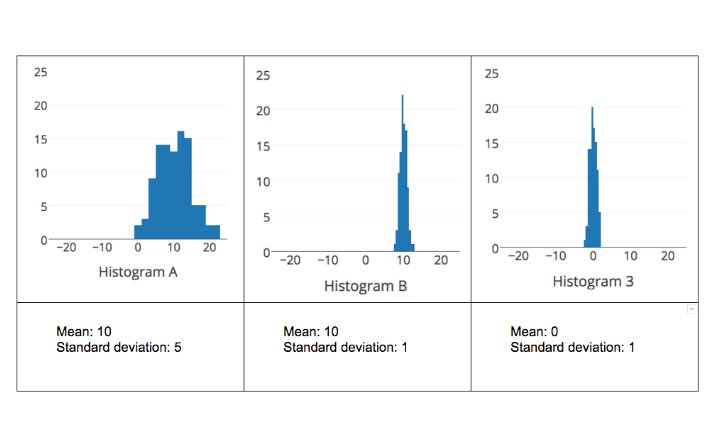
    • use range and density of points towards the center to describe the variability of a data set
    • use standard deviation to describe how range and variation are related to the mean
    • use a data set’s distribution to consider and justify where other data points may lie in relation to the mean
    • interpret the spread and mean of a statistical distribution.
  • interpret and describe connections between the frequency and distribution across different representations (graphs, tables, or charts)
    • Determine the extent to which the difference matters
    • Articulate the relationship between a normal distribution (a result of a continuous random variable) and a binomial distribution (a result of a discrete random variable).
    • Compare the experimental and theoretical probability of a sample space using areas in the distribution curve

Develop conceptual understanding:

statistics, univariate, measures of center, mean, median, mode, frequency, range, outlier, density, variability, standard deviation, distribution, spread, normal distribution, binomial distribution

Supporting terms to communicate:

data point, data set, independent, dependent, domain, range, random, sample, categorized, summarized, discrete, continuous
Core Resource

No Core Resource for this Big Idea.

Consider using the Instructional Routines linked below for teaching towards this Big Idea.