Evidence of Understanding
- explain patterns in the unit circle
- graph the unit circle and identify its center, radius, intercepts, domain, and range
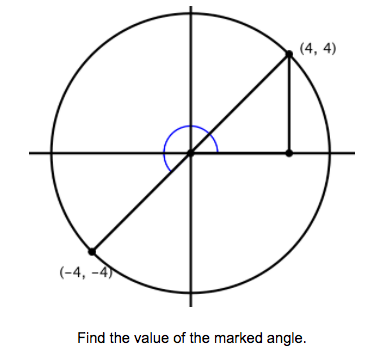
- use the unit circle’s radius to explain why 180o is equivalent to π
- create diagrams that illustrate equivalent degree and radian measures
- describe how degrees and radians are related
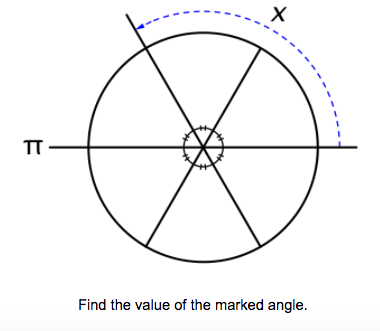
- convert between degrees and radians
- approximate the degree measure for a single radian
- use transformations and special triangles to find points on the unit circle for central angles that are multiples of 30o or 45o
- identify and justify relationships between coordinate points on the unit circle
- Example: describe how the coordinates of 30o and 60o are related, etc.
- describe the relationship between the angle measure and the sign value of its coordinates
- Example: any angle with a terminal side in the second quadrant has coordinates (-x, + y)
- prove the Pythagorean Identity sin2θ + cos2θ = 1
- justify coordinates on the unit circle as (cosθ, sinθ)
- justify coordinates on the unit circle as (cosθ, sinθ)
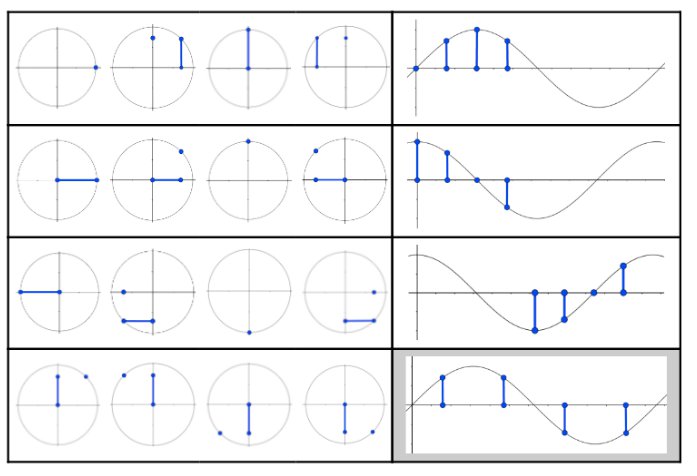
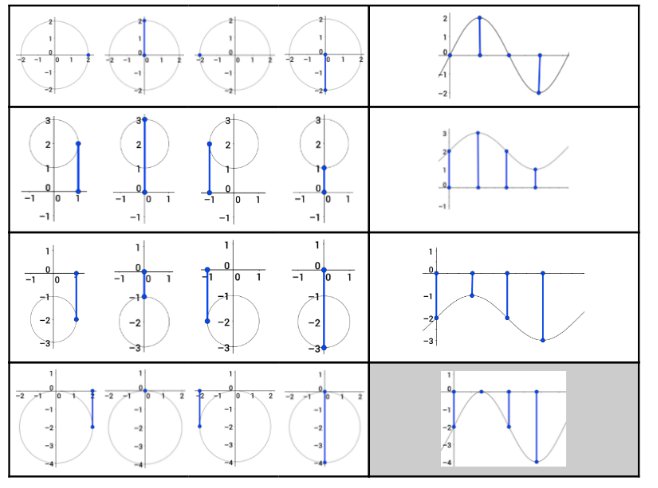
- use the unit circle to extend understanding of trigonometry
- justify intervals when values of sinθ or cosθ increase or decrease from a diagram or table
- explain why the sine or cosine of any angle must be between 1 and -1, inclusively
- determine the exact value of any sine, cosine, tangent, cosecant, secant, or cotangent expression for angles that are multiples of 30o or 45o
- use reference angles to evaluate a trig expression
- justify why the tangent of 90o and 270o are undefined
- explain why the tangent values are positive in quadrants 1 and 3
- approximate the value of any sin, cos, tan, csc, sec, or cot expression from the unit circle
- Example: sin163o is between ½ and 0 because sin163o falls between sin150o and sin180o, or sin163o is between ½ and 0 because the terminal side is in Q2 where y is positive and the right triangle‘s base angle is 17o and sin17o must be less than sin30o = ½
- use properties of the unit circle to solve for an unknown angle in a trig equation
Develop conceptual understanding:
unit circle, radian, Pythagorean Identity, tangent, cosecant, secant, cotangent, undefined
Supporting terms to communicate:
circle, center, radius, intercepts, domain, range, degree, special triangles, reflection, rotation, terminal side, quadrant, sine, cosine