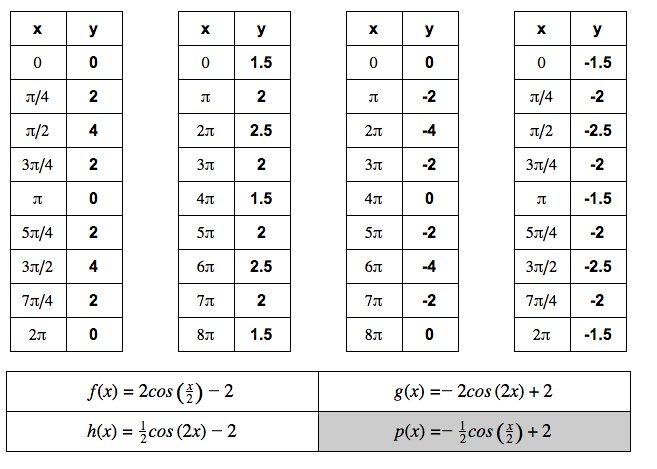
Evidence of Understanding

• interpret the features of a trig function from its graph, table, or equation
  • graph f(x) = sinx and g(x) = cosx and describe the relationship between inputs and outputs
    • given any input, use the graph to identify the output
  • identify the period, amplitude, midline, and frequency for any trig function
  • explain connections between the unit circle and sine, cosine, and tangent functions
    • describe restrictions on the domain and range
    • identify intervals that are increasing, decreasing, positive, and negative
  • represent trigonometric functions in multiple formats, including graphically, in table form, and as a function rule
    
• describe trig functions in relation to its parent function, f(x) = sinx, cosx, or tanx
  • given the parent graph and another trig graph, describe how a transformation on the parent function impacts the function’s amplitude, midline, period and/or frequency  
  • create a graph, table of values, or equation for a function from a stated transformation
  • write the function rule from the graph
  • possible extension: explore parent functions of f(x) = cscx, secx, or cotx and create a graph, table of values, or equation for a function from a stated transformation
    
• use trigonometric functions to model different contexts
  • solve a real-world situation by creating and using a trigonometric function rule, graph, or table
    • analyze values to justify a trigonometric function model (and not linear, quadratic, or exponential)
  • interpret solutions using trigonometric function models
    • accept and reject possible solutions based on the context of the situation and the limitations on  reasonable domain and range values

Develop conceptual understanding:

frequency

Supporting terms to communicate:

function, input, output, domain, range, angle, cosine, sine, tangent, unit circle, reference angle, period, amplitude, midline, undefined, asymptote, interval, parent function, transformation