Circles

9 Components
Initial Task
Square Peg
Big Ideas
Big Idea 1 Big Idea 2 Big Idea 3
Formative Assessment Lesson
Inscribing and Circumscribing Right Triangles
Re-engagement
Re-engagement for Unit 7
End of Unit Assessments
End of Unit Assessment for Unit 7 End of Unit Assessment Teacher Resources for GEO Unit 7 Find aligned Regents questions with Quiz Banker
Geo U6: Circles
Browse Components
Initial Task
Square Peg
Big Ideas
Big Idea 1 Big Idea 2 Big Idea 3
Formative Assessment Lesson
Inscribing and Circumscribing Right Triangles
Re-engagement
Re-engagement for Unit 7
End of Unit Assessments
End of Unit Assessment for Unit 7 End of Unit Assessment Teacher Resources for GEO Unit 7 Find aligned Regents questions with Quiz Banker
Big Idea:

Big Idea 2

There is a constant proportional relationship between an angle and its arc measures on a circle.

1 week
See Standards
Common Core: Major Standards:
G-SRT.B.5

Prove theorems involving similarity. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. Clarification: ASA, SAS, SSS, AAS, and Hypotenuse-Leg theorem are valid criteria for triangle congruence. AA, SAS, and SSS are valid criteria for triangle similarity.

Common Core: Supporting Standards:
G-CO.D.12

Make geometric constructions. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. Clarification: Constructions include but are not limited to the listed constructions. Example: constructing the median of a triangle or constructing an isosceles triangle with given lengths.

Common Core: Additional Standards:
G-C.B.5

Find arc lengths and areas of sectors of circles. Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.

G-C.A.2

Understand and apply theorems about circles. Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle.
Clarification: Relationships include but are not limited to the listed relationships. Example: angles involving tangents and secants.

Evidence of Understanding

  • describe proportional relationships between angles, arcs, and sectors of a circle
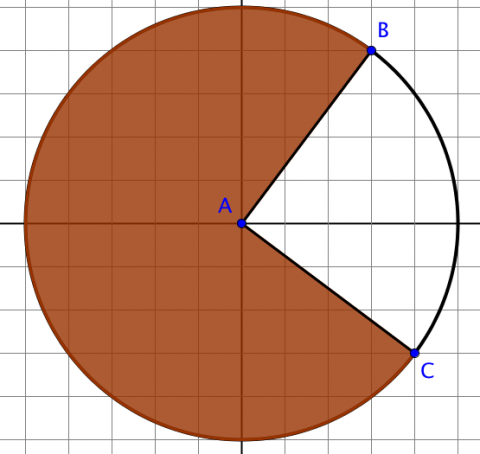
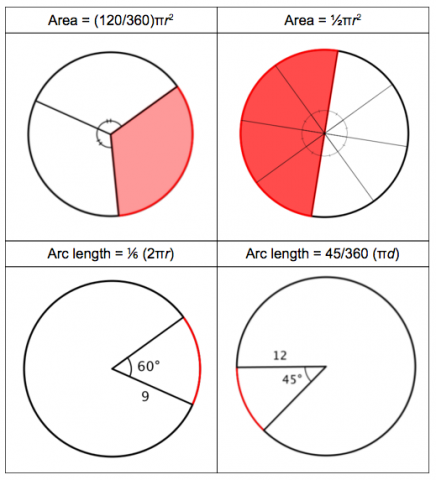
    • create visuals to describe a central angle in terms of the fraction of the circle it represents
      • Example: show an angle measuring 72° is equivalent to ⅕ of the circle
    • investigate the constant ratio between an angle’s arc length and a circle’s circumference
      • ​explain the proportional relationship with the radius
      • use similarity to derive the length of the arc intercepted by an angle
      • use tools to verify the relationship between an angle’s degree and radian measure
    • apply the relationship between degrees and radians to find a missing measure
      • determine and justify the length of 1 radian
    • explain how sectors are related to area of a circle using similarity relationships
      • derive and use the formula for determining the area of a sector
  • analyze and apply the relationships between the angles and arcs used to describe a circle
    • use examples and nonexamples to distinguish central, inscribed, and circumscribed angles
      • define and classify angles using radii, chords, and tangents
    • investigate relationships between angle and arc measure for a central, inscribed, or circumscribed angle and use them to solve problems
      • prove inscribed angles open to the same arc are congruent (and vice versa)
      • prove parallel chordsintercept congruent arcs
    • prove that a triangle inscribed in a circle with a leg through the center of the circle is a right triangle (hypotenuse is the diameter)
    • describe patterns relating the angle and arc measures on a circle by two tangents, two secants, a secant and a tangent, or a chord and a tangent
    • describe patterns relating the angle and arc measures resulting from two intersecting chords
    • calculate the value of an unknown angle or arc measure

Develop conceptual understanding:

central angle, arc length, circumference, degrees, radians, sector,  inscribed angle, circumscribed angle

Supporting terms to communicate:

equivalent, ratio, proportion, similarity, scale factor, dilation, angle, radius, diameter, area, chord, tangent, secant, parallel, alternate interior angles, hypotenuse

Core Resource

No Core Resource for this Big Idea.

Consider using the Instructional Routines linked below for teaching towards this Big Idea.

    Instructional Routine: Contemplate then Calculate
    These tasks are embedded within the instructional routine called Contemplate then Calculate.
    Instructional Routine: Connecting Representations
    These tasks are embedded within the instructional routine called Connecting Representations.