Evidence of Understanding
- describe an input in terms of its corresponding output
- approximate and justify the input of an exponential function given the output
- Example: given 59 = 2x, students recognize 2xas a continuous function and that 59 is between 32 and 64 and therefore x is a value between 5 and 6, closer to 6
- describe an exponential function in terms of the output, f(x), and its base
- Example: f(x) = 2x can be described as “base 2 is f(x) when raised to the exponent x” or “f(x) is equivalent to the base 2 raised to exponent x”
- use the outputs of an exponential function to graph its inverse function
- create and analyze a table of values for the inverse function
- describe the intercepts and end behavior of the inverse function
- approximate and justify the input of an exponential function given the output
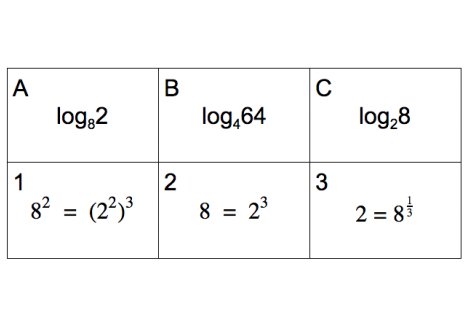
- create equivalent representations for exponential and logarithmic functions
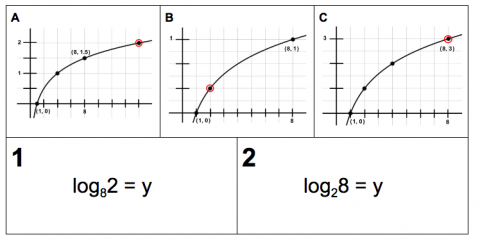
- analyze relationships between exponential and logarithmic equations using graphs or tables
- Example: compare Y= 2x, log2Y= X, and log2X = Y using features from their graphs
- recognize when equations model the same function, inverse functions, or neither
- create a table or graph from a simple logarithmic function rule (including natural logarithm)
- determine the output of a simple logarithm without a calculator (Example: log327 is 3 or log216 is 4 or log418 is a number slightly more than 2)
- create a simple exponential or logarithmic function rule that best models a given graph or table
- justify connections between features of the table, graph, and function rule of a given logarithm
- analyze relationships between exponential and logarithmic equations using graphs or tables
- illustrate exponentials and logarithms are inverse functions
- prove the composition of an exponential function and its inverse log function are commutative
- prove an exponential function and its inverse log function map onto one another over y = x
- describe how an exponential function is the reflection of its inverse log function
- algebraically solve for the inverse function rule for an exponential or log function
Develop conceptual understanding:
inverse, logarithm, natural logarithm
Supporting terms to communicate:
function, input, output, domain, range, exponential, base, e, natural base, intercept, end behavior, asymptote, inverse, commutative, reflect