Evidence of Understanding
- compare and contrast exponential functions with other functions that contain exponents
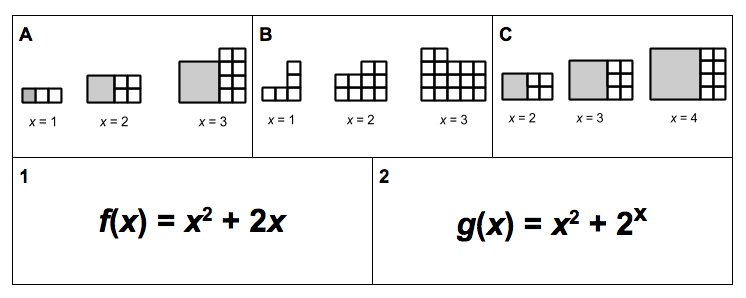
- describe similarities and differences between power and exponential models
- compare graphs of power functions and exponential functions (focus on y = x2 and y = 2x, y = x3 and y = 3x, and y =√x and y = ½x)
- possible extension: notice similarities between x2 and 2x and use that to anticipate and describe possible similarities between √x and the inverse of 2x
- generate and justify a function rule from a table, sequence, graph, or situation
- determine when a power, exponential, or neither function model is appropriate
- determine when a power, exponential, or neither function model is appropriate
- describe similarities and differences between power and exponential models
- investigate and transform expressions containing exponents into equivalent forms
- rewrite expressions using exponent properties am ● an = am + n (product), (am)n = amn (power), a0 = 1 (zero),am/an = am - n(quotient), and a-m = 1/am
- explore and describe the commutativity of exponent rules
- prove expressions with different bases are equivalent (Example: 643 = 86 = 49 = 218)
- explain the relationship between a rational exponent and its equivalent radical form
- connect the definition of a square root or cube root to its equivalent exponent
- convert between expressions with radicals and expressions with rational exponents
- rewrite expressions using exponent properties am ● an = am + n (product), (am)n = amn (power), a0 = 1 (zero),am/an = am - n(quotient), and a-m = 1/am
- analyze and evaluate expressions or equations using properties of exponents
- identify equations or expressions that can be rewritten with common bases to solve problems
- Example: solve 32x = 27x + 1 by rewriting as 32x = (33)x + 1or solve (1/16)x+ 13 = 77 by simplifying and rewriting as (2-4)x = 26
- evaluate expressions and solve equations using radicals or rational exponents
- Example: Evaluate 813/2 or 7√(1284) or Solve (5x - 2)5/3 - 1 = 31
- apply properties of exponents and common bases to evaluate without a calculator
- use rational exponents to determine an unknown base rate
- identify equations or expressions that can be rewritten with common bases to solve problems
Develop conceptual understanding:
power function, exponential function, exponent properties, commutative, base, exponent, rational exponent, radical form, square root, cube root
Supporting terms to communicate:
function, dependent, independent, input, output, domain, range, integer, rational number, equation, expression