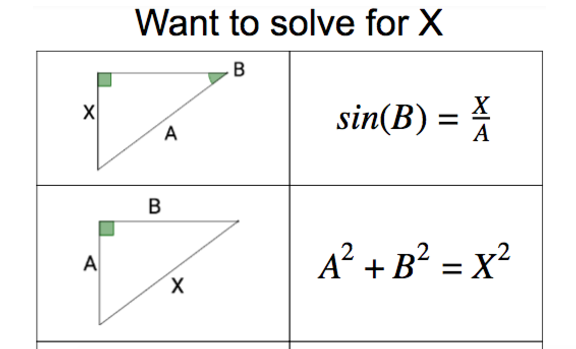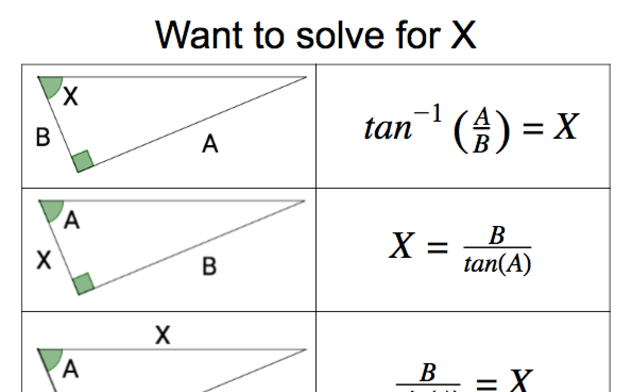Evidence of Understanding
- analyze characteristics of trigonometric ratios using right triangles
- use similarity, dilations, and scale factor to justify why a trigonometric ratio is constant
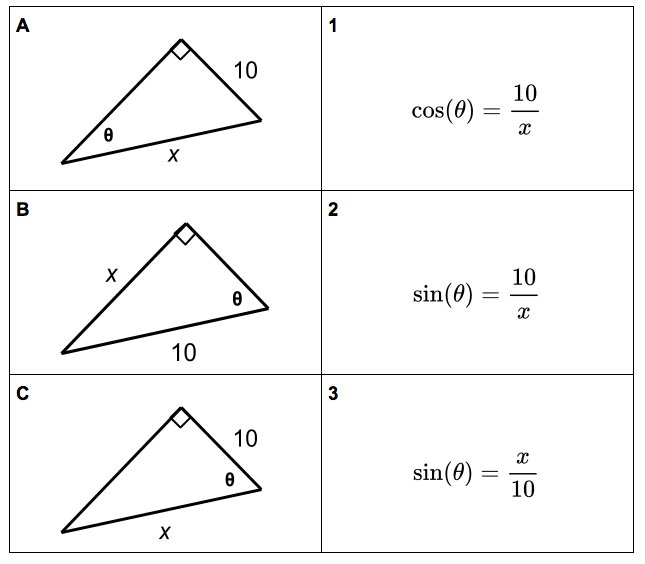
- analyze the legs of a right triangle to describe sine and cosine
- use the definition of the sine or cosine ratio to explain why neither value can exceed 1
- describe how increasing or decreasing one leg impacts the sine or cosine value
- explain how the sine and cosine of complementary angles are related and create an algebraic expression that generalizes the relationship between sine and cosine
- analyze the legs of a right triangle to describe the tangent
- use the definition of the tangent ratio to explain why the tangent values increases without limit as the angle increases
- describe features of a right triangle whose tangent is 1 (isosceles, 45-45-90)
- explain why the tangent of 45° is always 1
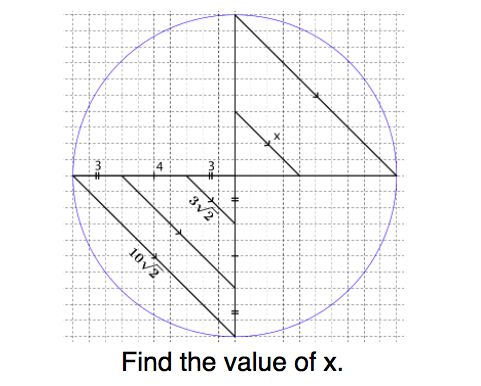
- use examples and nonexamples to make conjectures about special right triangles
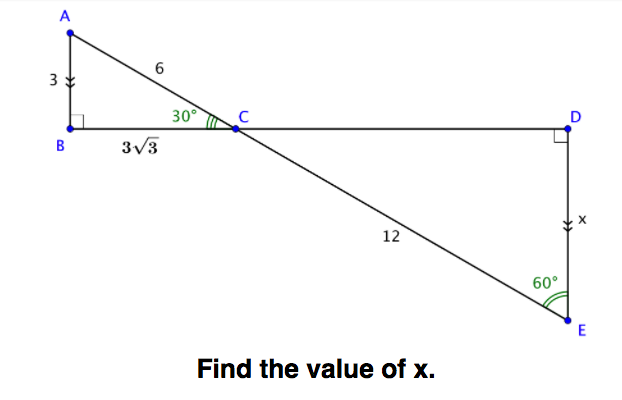
- the short side of a 30-60-90 triangle is always half the length of the hypotenuse
- the sine of 30° is always ½ and, conversely, if the sine is ½ then the angle is 30°
- the cosine of 60° is always ½ and, conversely, if the cosine is ½ then the angle is 60°
- determine the measure of angles or sides using right triangles and trigonometric ratios
- determine when to use Pythagorean Theorem or trig ratios (or a combination of methods) to solve right triangles
- create diagrams and write equations to model situations using right triangles
- recognize Pythagorean Theorem cannot be used to determine an unknown angle
- find the value of an unknown angle using inverse trig functions (sin-1, cos-1, and tan-1)
- determine the angle of depression or angle of elevation
- use special triangle patterns (30-60-90 and 45-45-90) to determine a missing measure
- find the area or perimeter of a simple polygon with right triangles using a variety of methods including trig, Pythagorean Theorem, special triangles, etc.
- determine when to use Pythagorean Theorem or trig ratios (or a combination of methods) to solve right triangles
Develop conceptual understanding:
trigonometric ratios, sine, cosine, tangent, special right triangle, inverse trig, angle of depression, angle of elevationSupporting terms to communicate:
constant ratio, similarity, scale factor, leg, side, opposite, adjacent, hypotenuse, corresponding, complementary, isosceles triangle