Evidence of Understanding
- describe the properties of a circle
- explore the relationship between a center point and a fixed distance (radius) rotated around it
- define a circle using the center, radius, and lines of symmetry
- use tools to inductively show the circumference of a circle is 2πr
- explain the relationship between the central angle of a circle and its arc measure
- describe a circle using 360o degrees and 2π radians or 180o and π radians
- describe a circle using 360o degrees and 2π radians or 180o and π radians
- explore the relationship between a center point and a fixed distance (radius) rotated around it
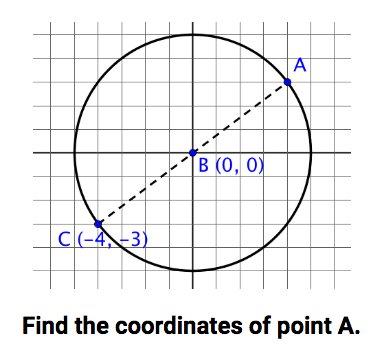
- graph the equation of a circle in the coordinate plane
- given any equation (x - h)2+ (y - k)2 = r2, describe how x, y, h, k, and r impact the graph
- find the center and the radius of a circle by completing the square
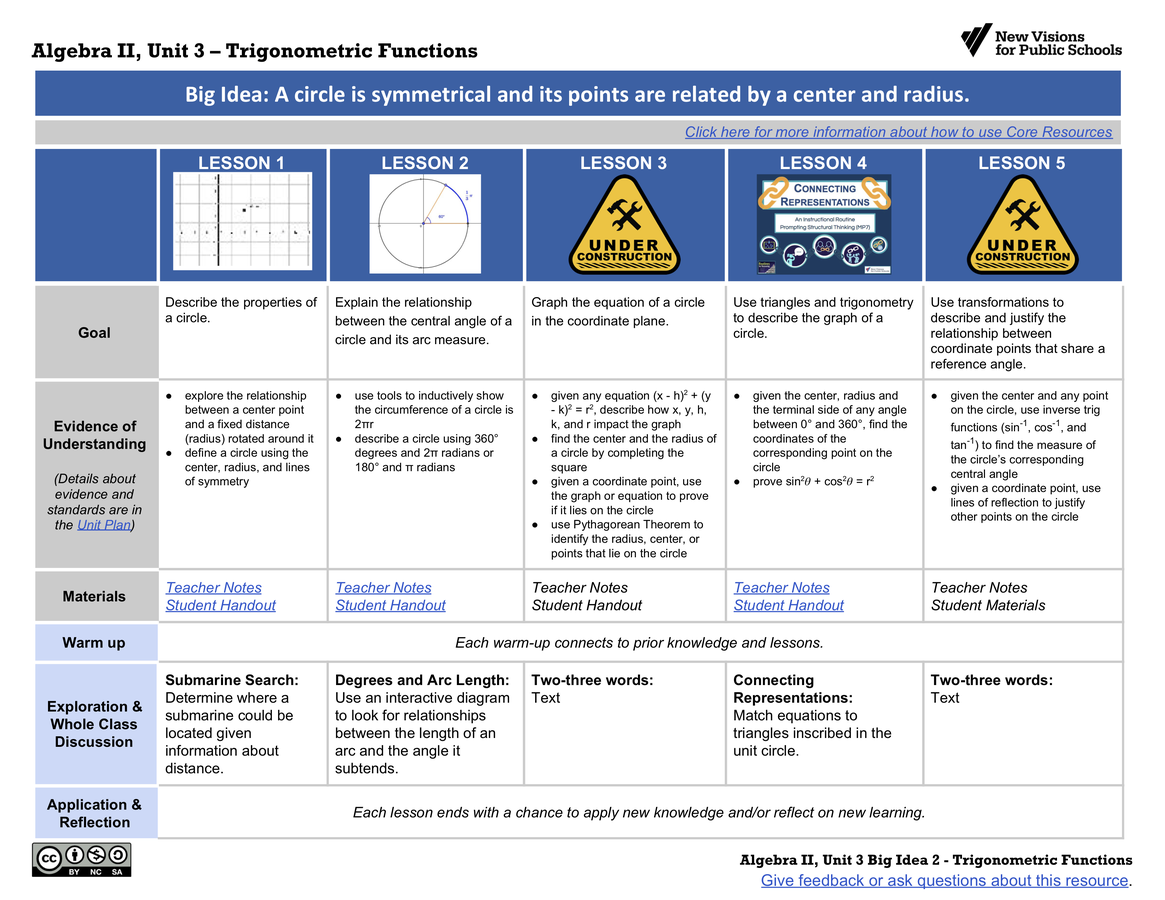
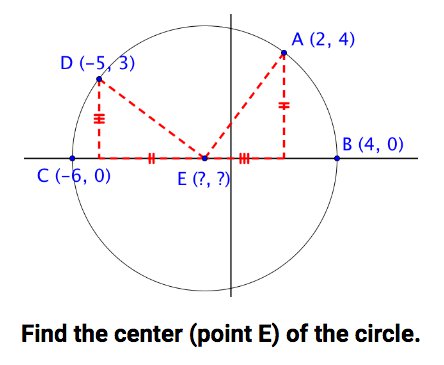
- given a coordinate point, use the graph or equation toprove if it lies on the circle
- given a coordinate point, use symmetry to justify other points on the circle
- use Pythagorean Theorem to identify the radius, center, or points that lie on the circle
- explain the connection of the equation of a circle and Pythagorean Theorem
- explain the connection of the equation of a circle and Pythagorean Theorem
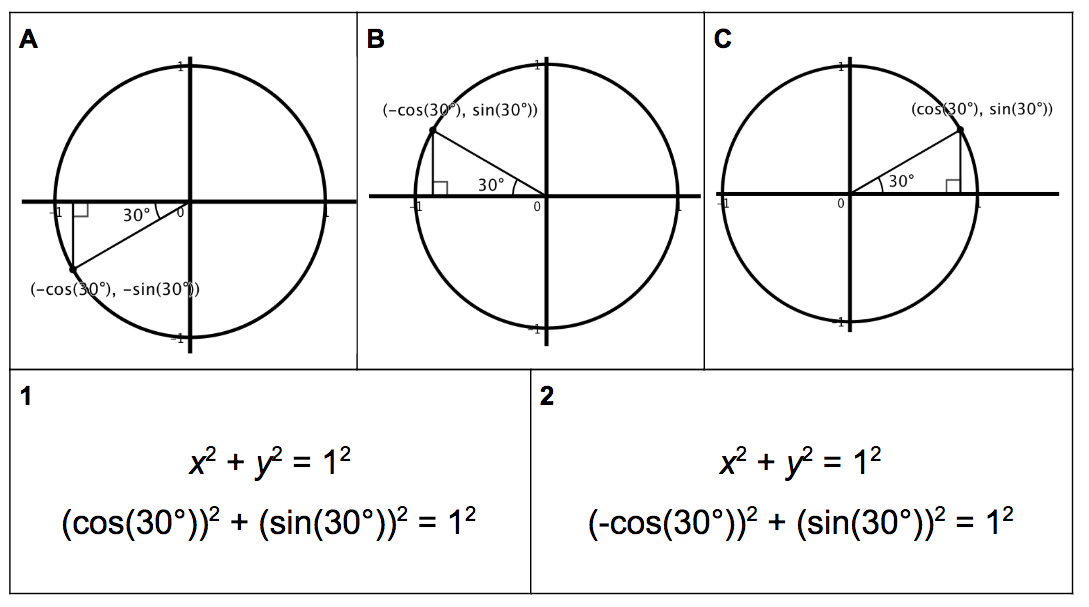
- use triangles and trigonometry to describe the graph of a circle
- given the center, radius and the terminal side of any angle between 0o and 360o , find the coordinates of the corresponding point on the circle
- use the properties of special right triangles (30-60-90 and 45-45-90)
- describe the relationship between cosine and the x coordinate of a point on the circle
- describe the relationship between sine and the y coordinate of a point on the circle
- prove sin2 θ + cos2 θ = 1
- use transformations to describe and justify the relationship between coordinate points that share a reference angle
- Ex: the points at 30o and 150o are similar because the right triangle is reflected
- Ex: the points 30o and 120o are similar because the right triangle is rotated
- given the center and any point on the circle, use inverse trig functions (sin-1, cos-1, and tan-1) to find the measure of the circle’s corresponding central angle
- given the center, radius and the terminal side of any angle between 0o and 360o , find the coordinates of the corresponding point on the circle
Develop conceptual understanding:
circle, circumference, arc measure, radian, terminal side, special right triangle (30-60-90 and 45-45-90), cosine, sine, reference angleSupporting terms to communicate:
center, radius, central angle, degrees, symmetrical, reflect, completing the square, quadrant, Pythagorean Theorem, right triangle, reflection, rotation, inverse trig