Evidence of Understanding
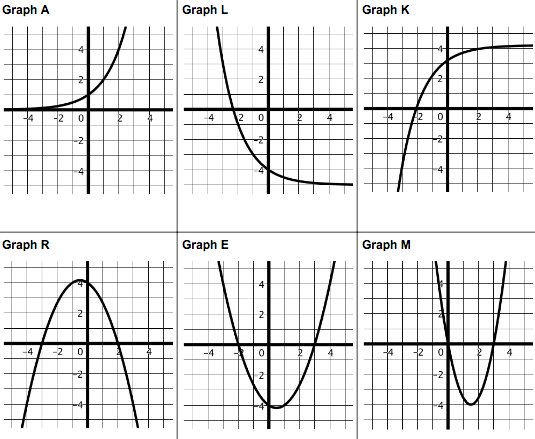
- compare the general shape and behavior of different function types
- identify intervals of a function that are increasing, decreasing, positive or negative
- use words, equations/inequalities, and interval notation
- generalize how intervals distinguish different function families (Example: quadratics always have one increasing interval and one decreasing interval)
- predict end behavior using a graph’s shape and the function’s rate(s) of change
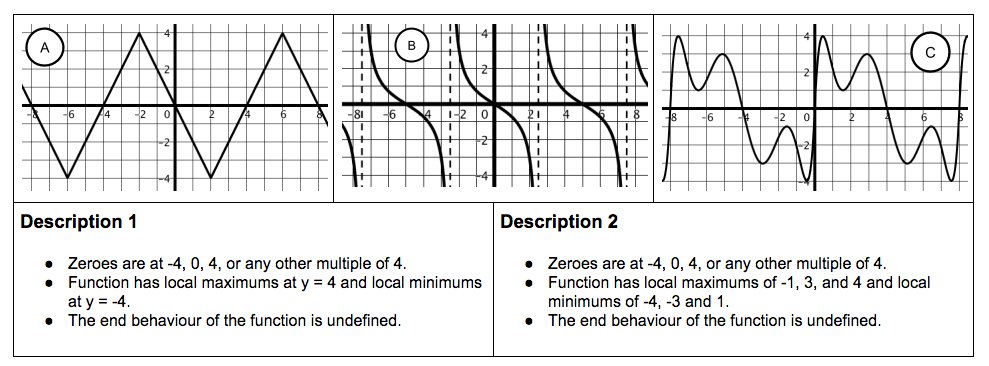
- explain why the end behavior of a periodic function is undefined
- use symmetry from a function’s graph or table to distinguish function families
- identify intervals of a function that are increasing, decreasing, positive or negative
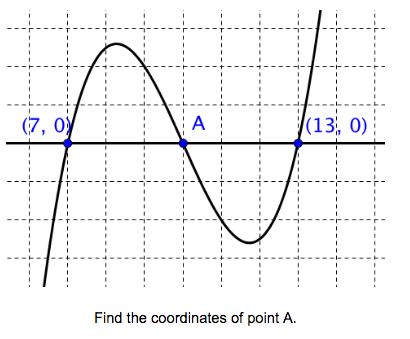
- identify and analyze points that determine the shape and behavior of a function’s graph
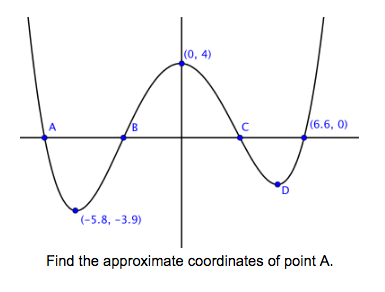
- determine exact integer zeros and approximate non-integer zeros from a graph or table
- recognize when a function is periodic and use the repetition to describe zeros of a periodic function
- recognize zeros (x intercepts) separate positive and negative intervals
- describe why critical points (mins and maxs) separate increasing and decreasing intervals
- use end behavior to distinguish relative from absolute mins and maxs
- create the graph for a given function rule using its intercepts, mins, maxs, and end behavior
- use tools strategically, especially graphing calculator features
- algebraically solve for key points of a linear or quadratic equation (using Algebra 1)
- determine exact integer zeros and approximate non-integer zeros from a graph or table
- determine a function’s family using its key points, shape, and end behavior
- describe and predict general features of critical points and zeros for each function family
- Example: cubics have at most 3 x-intercepts, quadratics always have 1 absolute min or max, etc.
- describe characteristics of a function’s graph or sketch the possible graph of a function given its characteristics
- recognize a periodic function from its undefined end behavior, repeating points or shape
- describe and predict general features of critical points and zeros for each function family
Develop conceptual understanding:
increasing interval, decreasing interval, positive interval, negative interval, end behavior, symmetry, zero, periodic function, critical point, relative or absolute min/max
Supporting terms to communicate:
linear, absolute value, quadratic, cubic, square root, cube root, polynomial, exponential, logarithmic, rational, piecewise, step function, integer