Tools of Geometry

12 Components
Initial Task
Transformer
Big Ideas
Big Idea 1 Big Idea 2 Big Idea 3 Big Idea 4 Big Idea 5
Formative Assessment Lesson
Representing & Combining Transformations
Re-engagement
Re-engagement for Unit 1
End of Unit Assessments
End of Unit Assessment for Unit 1 Performance Task for Unit 1 End of Unit Assessment Teacher Resources for GEO Unit 1 Find aligned Regents questions with Quiz Banker
Geo U1: Tools of Geometry
Browse Components
Initial Task
Transformer
Big Ideas
Big Idea 1 Big Idea 2 Big Idea 3 Big Idea 4 Big Idea 5
Formative Assessment Lesson
Representing & Combining Transformations
Re-engagement
Re-engagement for Unit 1
End of Unit Assessments
End of Unit Assessment for Unit 1 Performance Task for Unit 1 End of Unit Assessment Teacher Resources for GEO Unit 1 Find aligned Regents questions with Quiz Banker
Big Idea:

Big Idea 4

Corresponding parts of congruent polygons are congruent.

1 week
See Standards
Common Core: Major Standards:
G-CO.B.6

Understand congruence in terms of rigid motions. Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.

G-CO.B.7

Understand congruence in terms of rigid motions. Use the definition of congruence in terms of rigid motions to show that two triangles are congruent if and only if corresponding pairs of sides and corresponding pairs of angles are congruent.

Common Core: Supporting Standards:
G-CO.A.2

Experiment with transformations in the plane. Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch).

G-CO.A.4

Experiment with transformations in the plane. Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.

G-CO.A.5

Experiment with transformations in the plane. Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.

G-CO.D.12

Make geometric constructions. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. Clarification: Constructions include but are not limited to the listed constructions. Example: constructing the median of a triangle or constructing an isosceles triangle with given lengths.

Evidence of Understanding

  • describe qualities that make two polygons congruent or incongruent
    • identify corresponding parts (angles and sides) of polygons by annotating or redrawing
      • use tools (patty paper, paper folding, etc. to informally translate, reflect and/ or rotate) to map congruent polygons and place them “on top of” each other
      • use notation to signify congruence
    • use examples and non-examples to justifythat corresponding parts of congruent polygons and triangles are congruent (abbreviated as CPCTC for triangles)
    • explore whether equal perimeters or areas mean figures are congruent (or vice versa: if figures are congruent then decide if their perimeters or areas are equal)
  • justify two polygons are congruent using rigid motion transformations
    • justify, using tools, how congruent parts match after a rigid motion transformation
      • use notations to show corresponding parts between the pre-image to the image
      • use coordinate notation with the plane to describe rigid motion transformations
    • identify and use thecenter, degree, and direction of rotation to map a pre-image with its corresponding image
    • identify and use the line of reflection to map a pre-image with its corresponding image
      • generate or apply the equation of the line of reflection in the coordinate plane
      • use perpendicular bisectors to draw the line of reflection between a pre-image and its image, or draw the reflected image from a given pre-image and the line of reflection
    • translate an image and justify the preservation of distance and orientation
      • translate an angle by constructing parallel lines
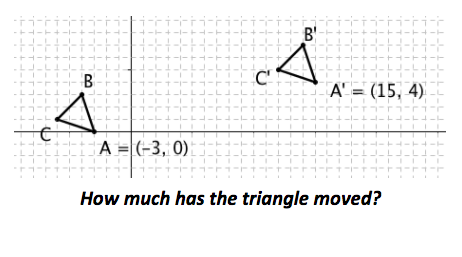
      • determine the translation vector between an image and pre-image (in space or the coordinate plane)
  • prove two figures are congruent using a sequence of transformations
    • describe the transformations that carry one figure onto another figure
    • draw transformed images given a sequence of transformations performed on a pre-image

Develop conceptual understanding:

corresponding parts, rigid motion transformations, center of rotation, perpendicular bisectors, pre-image, image, line of reflection, translation vector, parallel lines, sequence of transformations

Supporting terms to communicate:

polygon, translate, reflect, rotate, clockwise, counter-clockwise, congruent, map, carry, construct, function notation, input, output, preserve, orientation
Core Resource

A core resource supports multiple days of instruction.

  • Transforming Polygons
    This incomplete Core Resource supports students in extending what they know about transformations to transform general polygons.
    Resource:
    Transforming Polygons

    Geometry & Algebra II Archive

    Geo U1: Tools of Geometry

    Big Idea: Big Idea 4

    This incomplete Core Resource supports students in extending what they know about transformations to transform general polygons.

    Preview ResourceAdd a Copy of Resource to my Google Drive
    Type
    Geometry: Coordinate Geometry
    File
    Google Doc
    Tags
    congruence, polygons, transformations
    Standards
    Common Core: Major Standards ( G-CO.B.6, G-CO.B.7 ) Common Core: Supporting Sta…
    +— Details
    Common Core: Major Standards:
    G-CO.B.6

    Understand congruence in terms of rigid motions. Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.

    G-CO.B.7

    Understand congruence in terms of rigid motions. Use the definition of congruence in terms of rigid motions to show that two triangles are congruent if and only if corresponding pairs of sides and corresponding pairs of angles are congruent.

    Common Core: Supporting Standards:
    G-CO.A.2

    Experiment with transformations in the plane. Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch).

    G-CO.A.4

    Experiment with transformations in the plane. Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.

    G-CO.A.5

    Experiment with transformations in the plane. Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.

    G-CO.D.12

    Make geometric constructions. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. Clarification: Constructions include but are not limited to the listed constructions. Example: constructing the median of a triangle or constructing an isosceles triangle with given lengths.

    All Resources From:
Instructional Routine: Connecting Representations
These tasks are embedded within the instructional routine called Connecting Representations.
  • Reflections, Translations, Graphs, and Sentences
    Use visual structure of transformations for triangles to connect with sentence descriptions of transformations.
    Resource:
    Reflections, Translations, Graphs, and Sentences

    Geometry & Algebra II Archive

    Geo U1: Tools of Geometry

    Big Idea: Big Idea 4

    Use visual structure of transformations for triangles to connect with sentence descriptions of transformations.

    Preview ResourceAdd a Copy of Resource to my Google Drive
    Type
    Geometry: Tools of Geometry
    File
    Google Doc
    Tags
    instructional routine, connecting representations
    Standards
    Common Core: Major Standards ( G-CO.B.6, G-CO.B.7 ) Common Core: Supporting Sta…
    +— Details
    Common Core: Major Standards:
    G-CO.B.6

    Understand congruence in terms of rigid motions. Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.

    G-CO.B.7

    Understand congruence in terms of rigid motions. Use the definition of congruence in terms of rigid motions to show that two triangles are congruent if and only if corresponding pairs of sides and corresponding pairs of angles are congruent.

    Common Core: Supporting Standards:
    G-CO.A.2

    Experiment with transformations in the plane. Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch).

    G-CO.A.4

    Experiment with transformations in the plane. Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.

    G-CO.A.5

    Experiment with transformations in the plane. Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.

    G-CO.D.12

    Make geometric constructions. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. Clarification: Constructions include but are not limited to the listed constructions. Example: constructing the median of a triangle or constructing an isosceles triangle with given lengths.

    All Resources From: