- NV Math Team
- Getting Started
- Algebra I Archive
- 1: Curriculum Components
- 2: Instructional Routines
- 2A: Contemplate then Calculate
- 2B: Connecting Representations
- 2C: Group Learning Routines
- 2D: Additional Instructional Routines
- 3: ELL and SpEd Student Support
- A1 U0: Introduction to Algebra I
- A1 U1: Modeling with Functions
- A1 U2: Linear and Exponential Functions
- A1 U3: Linear Equations and Inequalities in One Variable
- A1 U4: Linear Equations and Inequalities in Two Variables
- A1 U5: Quadratic Functions
- A1 U6: Quadratic Equations
- A1 U7: Statistics
- Geometry & Algebra II Archive
- Geo U0: Introduction to Geometry
- Geo U1: Tools of Geometry
- Geo U2: Proofs about Congruence
- Geo U3: Similarity and Proof
- Geo U4: Right Triangle Trigonometry
- Geo U5: Extending to Three Dimensions
- Geo U6: Coordinate Geometry
- Geo U6: Circles
- A2 U0: Introduction to Algebra II
- A2 U1: Families of Functions
- A2 U2: Exponential Functions
- A2 U3: Trigonometric Functions
- A2 U4: Rational and Polynomial Functions
- A2 U5: Probability
- A2 U6: Statistics (Inferences from Data)
- Regents Readiness
- Find Resources
Find Resources
Search and browse resources for your classroom.
Use the filters below to see resources for a specific course, unit, and more.
- Common Core: Major Standards
- Common Core: Supporting Standards
- Common Core: Additional Standards
- Common Core: Practice Standards
Showing 15 Resources:

In this task, you must solve a problem about circles inscribed in squares.

Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

This incomplete Core Resource supports students in making connections between the Pythagorean theorem and the equation of circles.

Prove theorems involving similarity. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. Clarification: ASA, SAS, SSS, AAS, and Hypotenuse-Leg theorem are valid criteria for triangle congruence. AA, SAS, and SSS are valid criteria for triangle similarity.
Use coordinates to prove simple geometric theorems algebraically. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, 2).
Make geometric constructions. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line. Clarification: Constructions include but are not limited to the listed constructions. Example: constructing the median of a triangle or constructing an isosceles triangle with given lengths.
Understand and apply theorems about circles. Prove that all circles are similar.
Translate between the geometric description and the equation for a conic section. Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation.
Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

Connect visuals to arc length formulas involving the size of an angle.

Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

The slider allows the interior angles of the quadrilateral to change. the 4 interior angles of the quadrilateral are also organized with the same vertex (like a circle). As they interior angles of the quadrilateral change, the same 4 angles change in the circular format.

Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U2
Proofs about Congruence
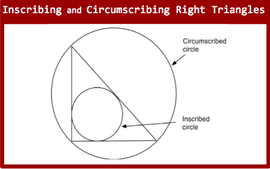
A Classroom Challenge (aka formative assessment lesson) is a classroom-ready lesson that supports formative assessment. The lesson’s approach first allows students to demonstrate their prior understandings and abilities in employing the mathematical practices, and then involves students in resolving their own difficulties and misconceptions through structured discussion.
Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

This problem introduces the circumcenter of a triangle and shows how it can be used to inscribe the triangle in a circle. It also shows that there cannot be more than one circumcenter.
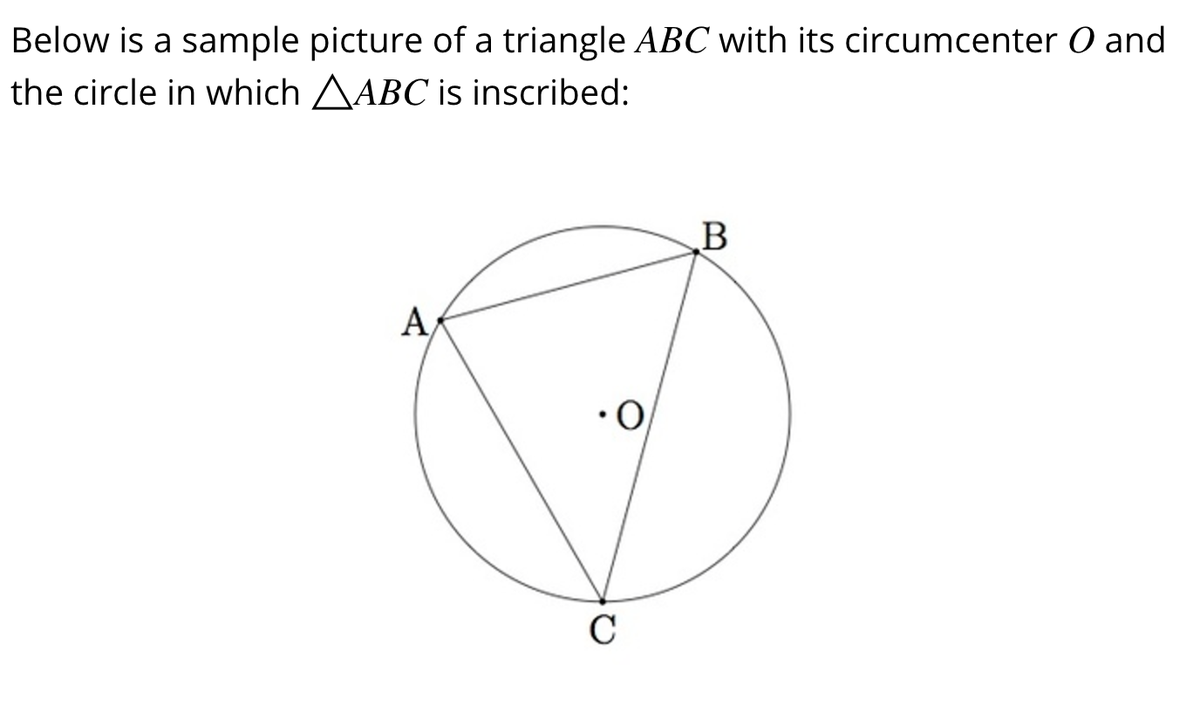
Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

This is a fun and inspiring description of someone's first conversation about the use of compasses - I think it could be a nice conversation at other early points in students exposure to compasses as well.
A note on math circles: Math Circles are a particular talk protocol for facilitating a discovery based conversation with a group of learners. Typically, there's a starting question and the facilitator responds to each student's contribution to the conversation with another question. It is common in math circles that the end result of the conversation is both more sophisticated and powerful than what happens in a typical math classroom, however it is hard to facilitate and requires that you be willing to go with what your students are thinking about. It also helps to have a great deal of mathematical knowledge, not to mention a very engaged group of learners.

Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U1
Tools of Geometry

3 Acts activity about the area of a sector.

Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

This task provides a context for connecting an angle in radians to the arc length intercepted by the angle.

Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

This task provides a good opportunity to use isosceles triangles and their properties to show an interesting and important result about triangles inscribed in a circle with one side of the triangle a diameter: the fact that these triangles are always right triangles is often referred to as Thales' theorem. It does not have a lot of formal prerequisites, just the knowledge that the sum of the three angles in a triangle is 180 degrees.
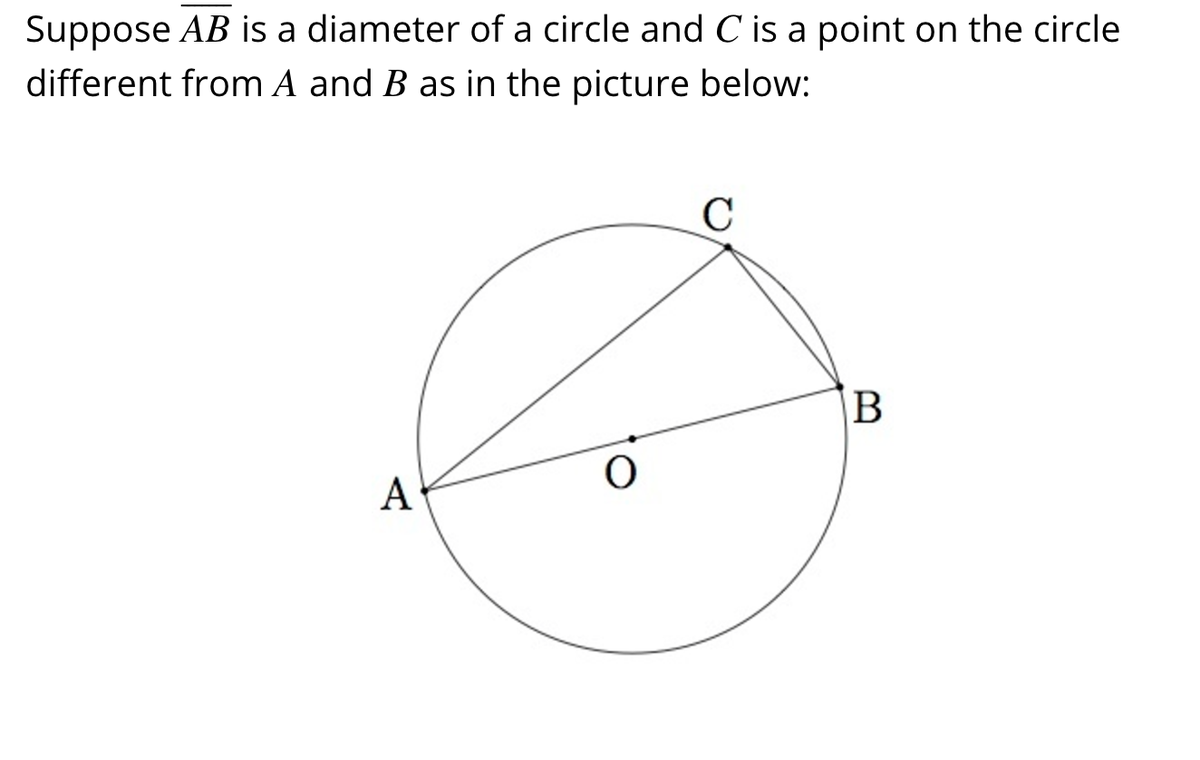
Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

The result here complements the fact, presented in the task ''Right triangles inscribed in circles I,'' that any triangle inscribed in a circle with one side being a diameter of the circle is a right triangle. A second common proof of this result rotates the triangle by 180 degrees about M and then shows that the quadrilateral, obtained by taking the union of these two triangles, is a rectangle.

Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles

The goal of this task is to work on showing that all circles are similar using these two different methods, the first visual and the second algebraic.

Teacher Feedback
Please comment below with questions, feedback, suggestions, or descriptions of your experience using this resource with students.
- Geo U6
Circles